如图所示，光滑的斜面$abcd$是边长为$L$的正方形，其倾角$\theta$为未知量，在$a$点给小球（可视为质点）一个由$a$指向$b$的初速度$v_{0}$，小球沿斜面运动到$c$点，重力加速度为$g$，空气阻力不计。下列说法正确的是$(\qquad)$

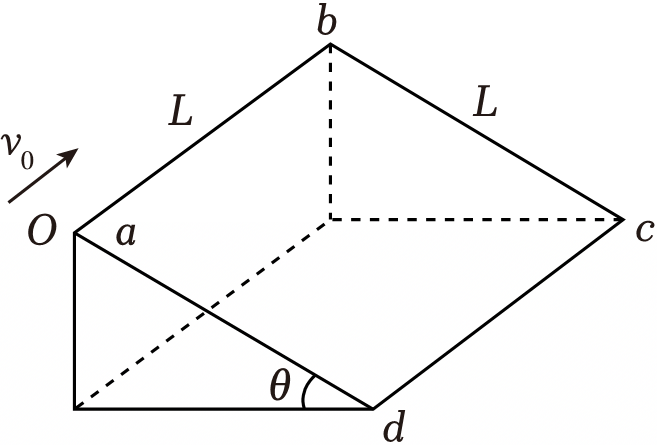
小球从$a$到$c$的运动时间为$\\dfrac{2L}{v_{0}}$

小球从$a$到$c$的平均速度大小为$2v_{0}$

斜面倾角$\\theta$的正弦值为$\\dfrac{2v_{0}^{2}}{gL}$

小球在$c$点速度方向与$cd$边间夹角的正切值为$\\dfrac{\\sqrt{5}}{2}$

$\rm A$、由类平抛运动的规律，可知在水平方向上，小球从$a$到$c$的运动为匀速运动，即时间$t=\dfrac{L}{v_{0}}$，故$\rm A$错误；

$\rm B$、由几何关系，可知小球从$a$到$c$的位移为$s=\sqrt{2}L$，则平均速度为$\overline{v}=\dfrac{s}{t}$，解得：$\overline{v}=\sqrt{2}v_{0}$，故$\rm B$错误；

$\rm C$、由类平抛运动的规律，在沿斜面方向：$L=\dfrac{1}{2}at^{2}$，$a=g\sin\theta$，结合$\rm A$选项分析，可知时间$t$，联立解得：$\sin\theta=\dfrac{2v_{0}^{2}}{gL}$，故$\rm C$正确；

$\rm D$、设小球在$c$点速度与$dc$的夹角为$\beta$，在沿斜面方向：$v_{y}=at$，$\tan\beta= \dfrac{v_{y}}{v_{0}}$，解得：$\tan\beta=2$，故$\rm D$错误。

故选：$\rm C$。