如图所示，将质量为$m$的小球从倾角$\theta=30^\circ$的光滑斜面上$A$点以速度$v_{0}=10\;\rm m/s$水平抛出（即$v_{0}//CD$），小球运动到$B$点，已知$AB$间的高度$h=5\;\rm m$，重力加速度$g$取$10\;\rm m/s^{2}$，则小球从$A$点运动到$B$点所用的时间和到达$B$点时的速度大小分别为$(\qquad)$

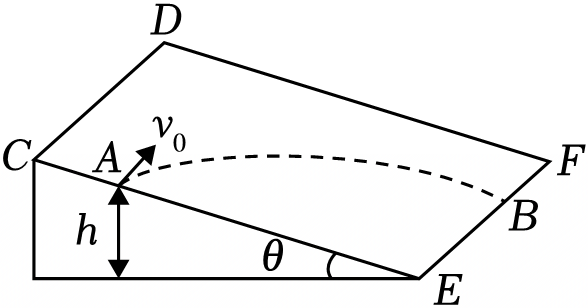
$1\\;\\rm s$    $20\\;\\rm m/s$

$1\\;\\rm s$    $10\\sqrt{2}\\;\\rm m/s$

$2\\;\\rm s$    $20\\;\\rm m/s$

$2\\;\\rm s$    $10\\sqrt{2}\\;\\rm m/s$

根据牛顿第二定律得，小球沿斜面下滑的加速度为：

$a= \dfrac{mg\sin\theta}{m} =g\sin\theta=10\times 5\;\rm m/s^{2}=5\;\rm m/s^{2}$，

根据位移$—$时间关系可得：$\dfrac{h}{\sin\theta}=\dfrac{1}{2}at^{2}$

代入数据解得：$t=2\;\rm s$

沿斜面方向的速度大小为：$v_{y}=at=5\times 2\;\rm m/s=10\;\rm m/s$

则到达$B$点时的速度大小$v= \sqrt{v_{0}^{2}+v_{y}^{2}}=\sqrt{10^{2}+10^{2}}\;\rm m/s=10\sqrt{2}\;m/s$，故$\rm D$正确、$\rm ABC$错误。

故选：$\rm D$。