如图（$a$）所示为一款滑杆运输装置自动回拉系统，滑杆与水平面的夹角为$30^\circ$，滑杆上套着一质量$m=1.0\;\rm kg$的小球（可视为质点）。某次测试中，该系统向小球提供沿滑杆方向的外力$F$，小球从$A$点静止出发，规定沿滑杆向上为$F$的正方向，$F$随小球与$A$点间距离$x$的变化关系如图（$b$）所示，小球所受摩擦力可忽略不计，$g$取$10\;\rm m/s^{2}$，则小球$(\qquad)$

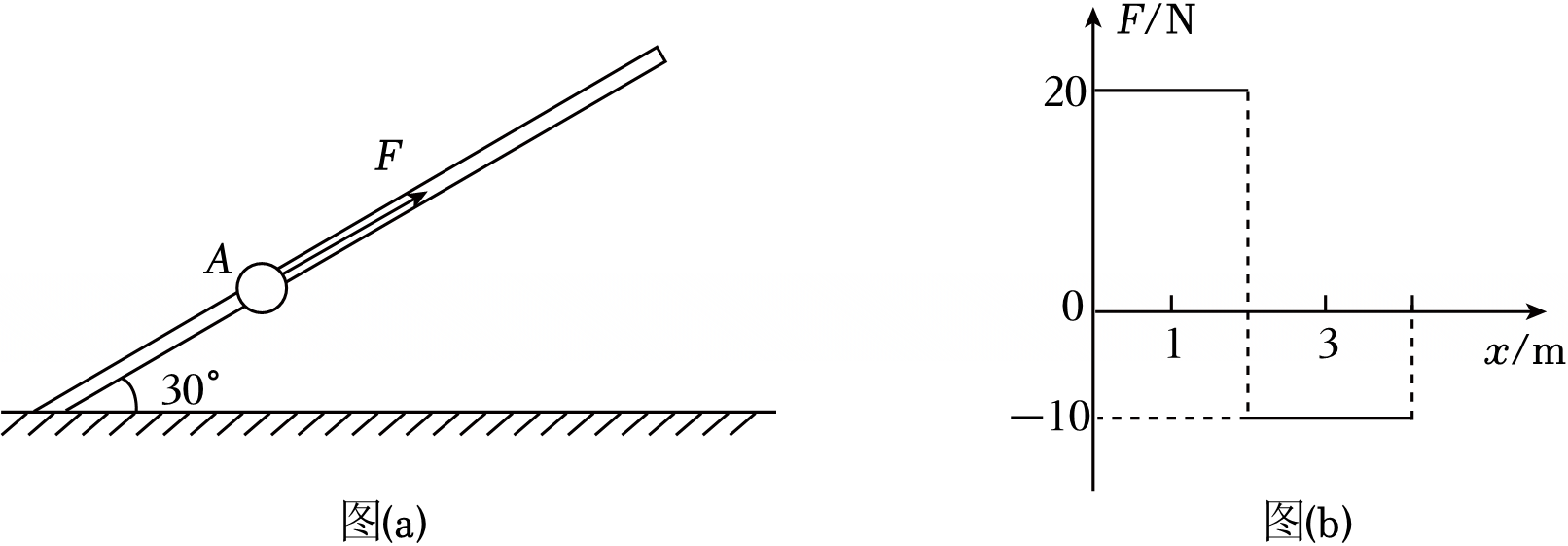
从$A$点开始$0\\sim 2\\;\\rm m$运动过程中加速度大小为$10\\;\\rm m/s^{2}$

在$x=4\\;\\rm m$时速度大小为$0$

从$A$点开始$0\\sim 2\\;\\rm m$运动的时间大于$2\\sim 4\\;\\rm m$的时间

从$A$点开始$0\\sim 2\\;\\rm m$运动的时间小于$2\\sim 4\\;\\rm m$的时间

$\rm A$．$0\sim 2\;\rm m$运动过程中沿杆方向受力分析$F-mg\sin30^{\circ}=ma_{1}$

解得$a_{1}=15\;\rm m/s^{2}$，故$\rm A$错误；

$\rm BCD$．$2\sim 4\;\rm m$运动过程中沿杆方向受力分析$F+mg\sin30^\circ=ma_{2}$

解得$a_{2}=-15\;\rm m/s^{2}$

运动到$2\;\rm m$时的时间$t_{1}=\sqrt{\dfrac{2x}{a_{1}}}$，解得$t_{1}=\dfrac{2}{\sqrt{15}}\;\rm s$

运动到$2\;\rm m$时的速度$v_{2}=a_{1}t_{1}$，解得$v_{2}=2\sqrt{15}\;\rm m/s$

由$x=v_{2}t_{2}+\dfrac{1}{2}a_{2}t_{2}^{2}$可得$2\sim 4\;\rm m$的运动时间$t_{2}=\dfrac{2}{\sqrt{15}}\;\rm s$，即从$A$点开始$0\sim 2\;\rm m$运动的时间小于$2\sim 4\;\rm m$的时间，由$v=v_{2}+a_{2}t_{2}$可得$x=4\;\rm m$的速度$v=0$，故$\rm B$正确，$\rm CD$错误。

故选：$\rm B$。