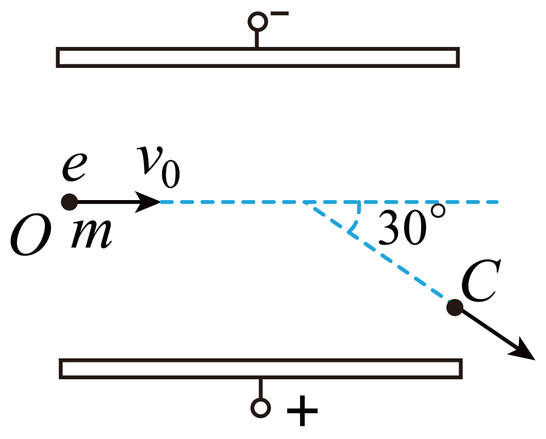
电子在$C$点时的动能是多少？

$9.7\\times10^{-18}\\;\\rm J$

电子在$C$点时的速度$v=\dfrac{v_{0}}{\cos 30{^\circ}}$

电子在$C$点时的动能$E_{\text{k}}=\dfrac{1}{2}mv^{2}=\dfrac{1}{2}m{\left(\dfrac{v_{0}}{\cos 30{^\circ}}\right)}^{2} \approx 9.7 \times 10^{- 18}\;\rm \text{J}$

电子从$O$到$C$的过程中在垂直极板方向上的位移？

$1.73\\;\\rm m$

电子在水平方向做匀速直线运动，运动时间$t=\dfrac{L}{v_{0}}=\dfrac{6}{4 \times 10^{6}}\;\rm \text{s}=1.5 \times 10^{- 6}\;\rm \text{s}$

垂直方向的分速度$v_{y}=v_{0}\tan 30^\circ $，根据$y=\dfrac{1}{2}at^{2}$

又$v_{y}=at$，则$y=\dfrac{1}{2}v_{y}t=\dfrac{1}{2}tv_{0}\tan 30{^\circ}$

代入数据得$y=\sqrt{3}\;\rm \text{m} \approx 1.73\;\rm \text{m}$

$O$、$C$两点间的电势差大小是多少$V$？

$15.125\\;\\rm V$

根据动能定理$eU_{OC}=\Delta E_{\text{k}}=E_{\text{kC}}-\dfrac{1}{2}mv_{0}^{2}$

代入数据得$eU_{OC}=9.7 \times 10^{- 18}-\dfrac{1}{2} \times 0.91 \times 10^{- 30} \times {(4 \times 10^{6})}^{2}\;\rm \text{J}=2.42 \times 10^{- 18}\;\rm \text{J}$

则$U_{OC}=\dfrac{2.42 \times 10^{- 18}}{e}\text{V}=15.125\;\rm \text{V}$