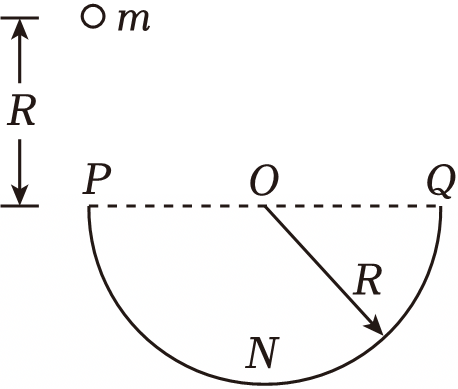
如图所示，一半径为$R$、粗糙程度处处相同的半圆形轨道竖直固定放置，直径$POQ$水平。一质量为$m$的质点从$P$点上方高为$R$处由静止开始下落，恰好从$P$点进入轨道。质点滑到轨道最低点$N$时，对轨道的压力为$4mg$，$g$为重力加速度的大小。用$W$表示质点从$P$点运动到$N$点的过程中克服摩擦力所做的功，则$(\qquad)$

$W= \\dfrac{1}{2}mgR$，质点恰好可以到达$Q$点

$W= \\dfrac{1}{2}mgR$，质点不能到达$Q$点

$W= \\dfrac{1}{2}mgR$，质点到达$Q$点后，继续上升一段距离

$W\\lt \\dfrac{1}{2}mgR$，质点到达$Q$点后，继续上升一段距离

在$N$点时对质点受力分析，根据牛顿第二定律得$F_{N}-mg=\dfrac{mv^{2}}{R}$

解得$v= \sqrt{3gR}$

则从开始下落到$N$点过程，根据动能定理可得$mg \cdot 2R-W=\dfrac{1}{2}mv^{2}$

解得$W= \dfrac{1}{2}mgR$

由于摩擦力做负功，故质点在半圆轨道上相同高度时在$NQ$上的速度小于在$PN$上的速度，所以质点对轨道的压力也较小，那么摩擦力也较小，所以质点从$N$到$Q$克服摩擦力做的功$W'\lt W= \dfrac{1}{2}mgR$

从开始下落到$Q$点过程中有动能定理$E_{{\rm k}Q}=mgR-W-W'\gt0$

可知质点到达$Q$后，继续上升一段距离，故$\rm C$正确，$\rm ABD$错误。

故选：$\rm C$。