高中 | 带电粒子在匀强电场中的偏转运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在匀强电场中的偏转运动
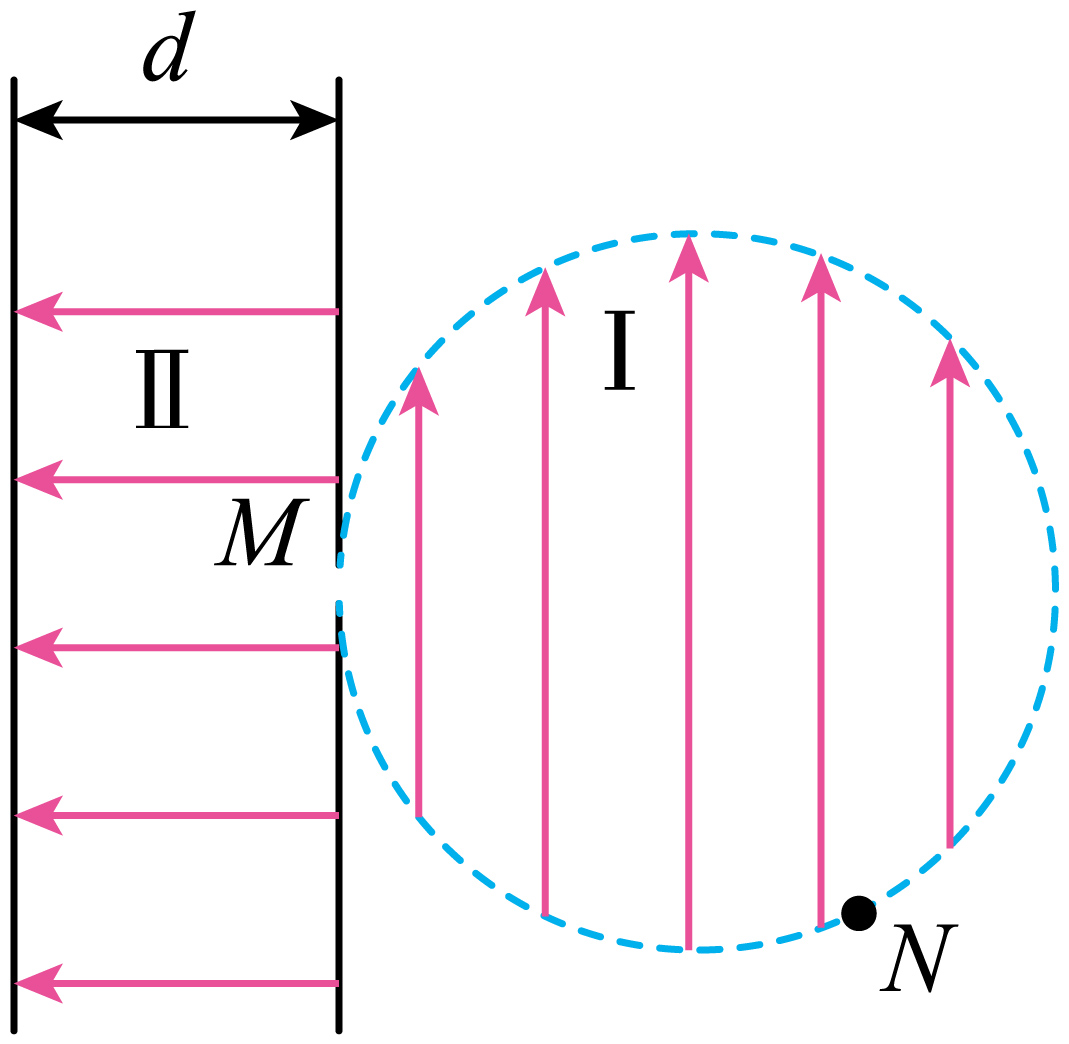
如图所示,圆形区域内存在竖直向上的匀强电场Ⅰ;圆形区域左侧有两正对竖直放置的平行金属板,板间存在水平向左的匀强电场Ⅱ;右金属板与圆形区域相切于$M$处,相切处有一小孔。现让一质量为$m$、电荷量绝对值为$q$的带电粒子,从圆边界上的$N$点以一定速度进入电场Ⅰ,恰好从$M$点垂直金属板进入电场Ⅱ,刚好能到达左金属板。已知电场Ⅰ、Ⅱ的电场强度大小均为$E$,金属板间的距离为$d$,带电粒子在$N$点的速度大小是$M$点的$2$倍,带电粒子的重力和空气阻力忽略不计。求:
粒子进入电场Ⅱ的速度大小$v_{0}$;
$\\sqrt{\\dfrac{2qEd}{m}}$
"]]在电场Ⅱ中,根据运动分析,粒子带负电
根据动能定理,有$- qEd=0-\dfrac{1}{2}mv_{0}^{2}$
解得$v_{0}=\sqrt{\dfrac{2qEd}{m}}$
$MN$两点间的电势差$U_{MN}$;
$-3Ed$
"]]从$M$到$N$,根据动能定理,有$- qU_{MN}=\dfrac{1}{2}m\left( 2v_{0} \right)^{2}- \dfrac{1}{2}mv_{0}^{2}$
联立解得$U_{MN}=-3Ed$
粒子在两电场中运动的总时间$t$。
$\\left( \\sqrt{3}+1 \\right)\\sqrt{\\dfrac{2md}{qE}}$
"]]根据$U_{MN}=-3Ed=−Eh$
可知$M$、$N$两点间的竖直距离为$h=3d$
带电粒子在$N$点的速度大小是$M$点的$2$倍,可得粒子在$N$点时竖直方向的分速度为$v'=\sqrt{\left( 2v_{0} \right)^{2}-v_{0}^{2}}=\sqrt{3}v_{0}$
粒子在电场Ⅰ中,有$3d=\dfrac{v'}{2}t_{1}$
粒子在电场Ⅱ中,有$d=\dfrac{v_{0}}{2}t_{2}$
粒子在两电场中运动的总时间$t=t_{1}+t_{2}$
联立解得$t=\left( \sqrt{3}+1 \right)\sqrt{\dfrac{2md}{qE}}$
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析(完整版)
