高中 | 螺旋测微器的读数和使用 题目答案及解析
稿件来源:高途
高中 | 螺旋测微器的读数和使用题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.6 导体的电阻
螺旋测微器的读数和使用
小球在液体中运动时要受到液体的摩擦阻力,这种阻力称为粘滞力或内摩擦力。在一般情况下,半径为$r$ 的小球以速度$v$在液体中运动时,所受的液体阻力可用斯托克斯公式$f=6\pi\eta rv$表示,式中$\eta$称为液体的粘滞系数(也叫“内摩擦因数”,其国际单位为$\rm Pa ⋅ s$),$r$为小球半径,$v$为小球运动的速度。某兴趣小组根据所掌握的知识,搜集器材设计了如图甲所示的实验,测定某液体的粘滞系数$\eta$,实验操作如下:
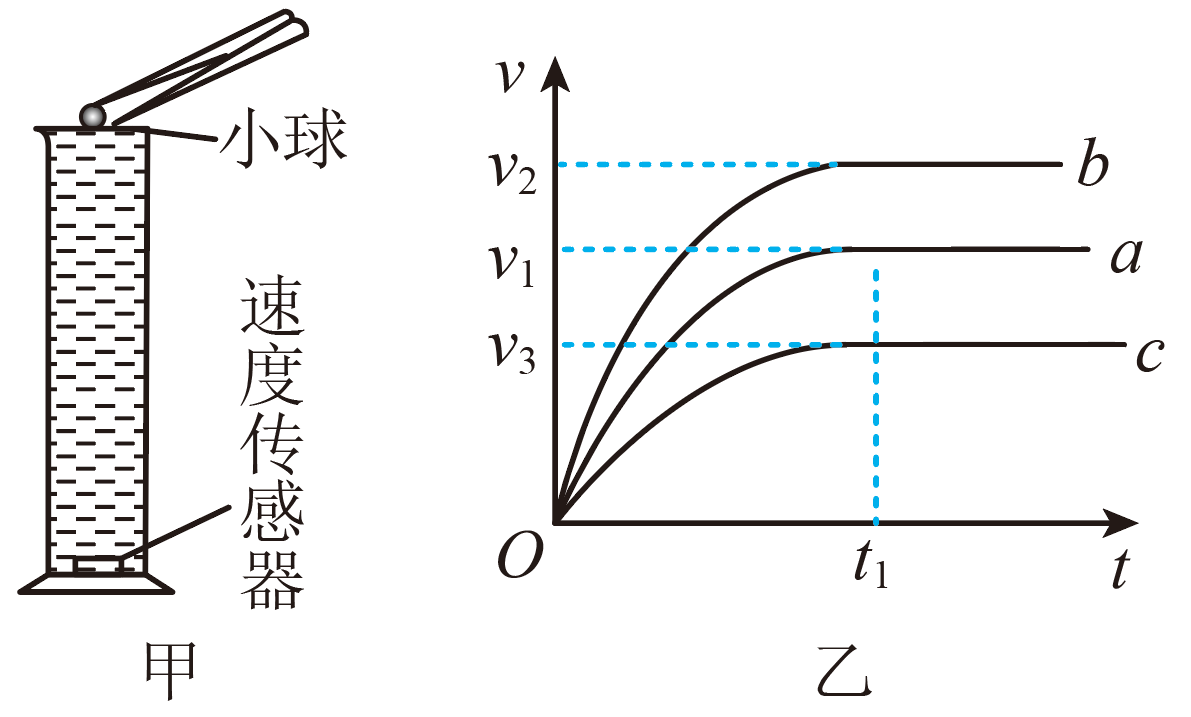
①将无线防水速度传感器安装在足够长量筒底部,传感器与计算机(图中未画出)建立联系,待测液体注满量筒;
②用螺旋测微器测定小球直径$D$;
③根据小球材质和液体种类查出它们的密度分别为$\rho$和$\rho_{0}$;
④用镊子将小球轻放在液体中让其在液体中下落,同时用计算机记录小球下落速度随时间变化的$v-t$ 图像如图乙中曲线$a$;
⑤改变液体的温度,重复④步骤操作,得到不同的$v-t$ 图像如图乙中曲线$b$、$c$。
螺旋测微器读数如图丙所示,小球直径$D=$ $\;\rm mm$;
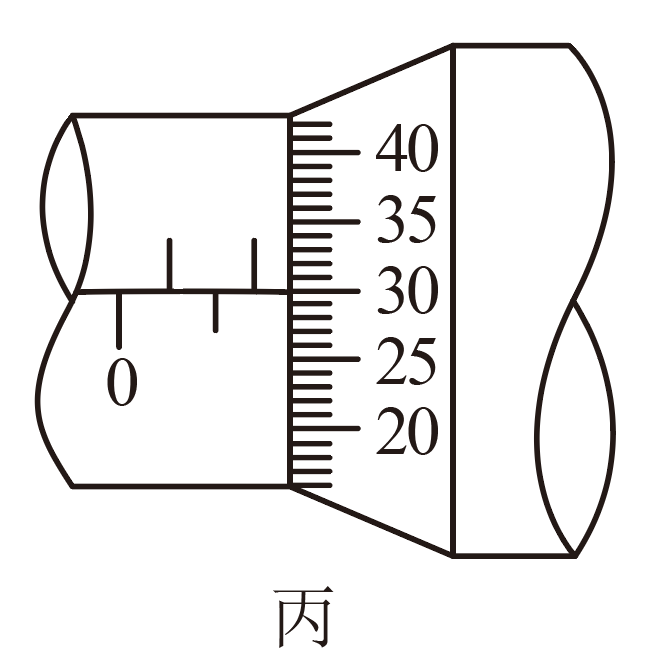
螺旋测微器读数是固定刻度读数($0.5\;\rm mm$的整数倍)加可动刻度($0.5\;\rm mm$以下的小数)读数,图中读数为$D=1.5\;\rm mm+30.0 \times 0.01\;\rm mm=1.800\;\rm mm$
查得小球的密度$\rho=8.5 \times 10^{3}\;\rm kg/m^{3}$ ,液体的密度$\rho_{0}=1.3 \times 10^{3}\;\rm kg/m^{3}$ ,测得小球匀速下落速度$v_{1}=2 \times 10^{-2}\;\rm m/s$,则该液体的粘滞系数$\eta=$ $\;\rm Pa ⋅ s$(重力加速度$g$取$10\;\rm m/s^{2}$,结果保留三位有效数字);
小球的体积为$V=\dfrac{4}{3}\pi r^{3}=\dfrac{1}{6}\pi D^{3}$
由粘滞力随速度增大而增大可知,小球加速度先减小后为零,加速度为零时有$\rho Vg-\rho_{0}Vg-6\pi\eta rv_{1}=0$
联立方程,解得$\eta=\dfrac{\left( \rho-\rho_{0} \right)gD^{2}}{18v_{1}}$
带入数据得$\eta=0.648\;\rm Pa ⋅ s$
已知当温度升高时,液体的粘滞系数减小,由此可判断图线$a$、$b$、$c$对应的液体温度$T_{a}$、$T_{b}$、$T_{c}$ 的关系是 。
由粘滞系数表达式可知,粘滞系数越小,小球的收尾速度越大,温度越高,因此$T_{b}\gt T_{a}\gt T_{c}$
高中 | 螺旋测微器的读数和使用题目答案及解析(完整版)
