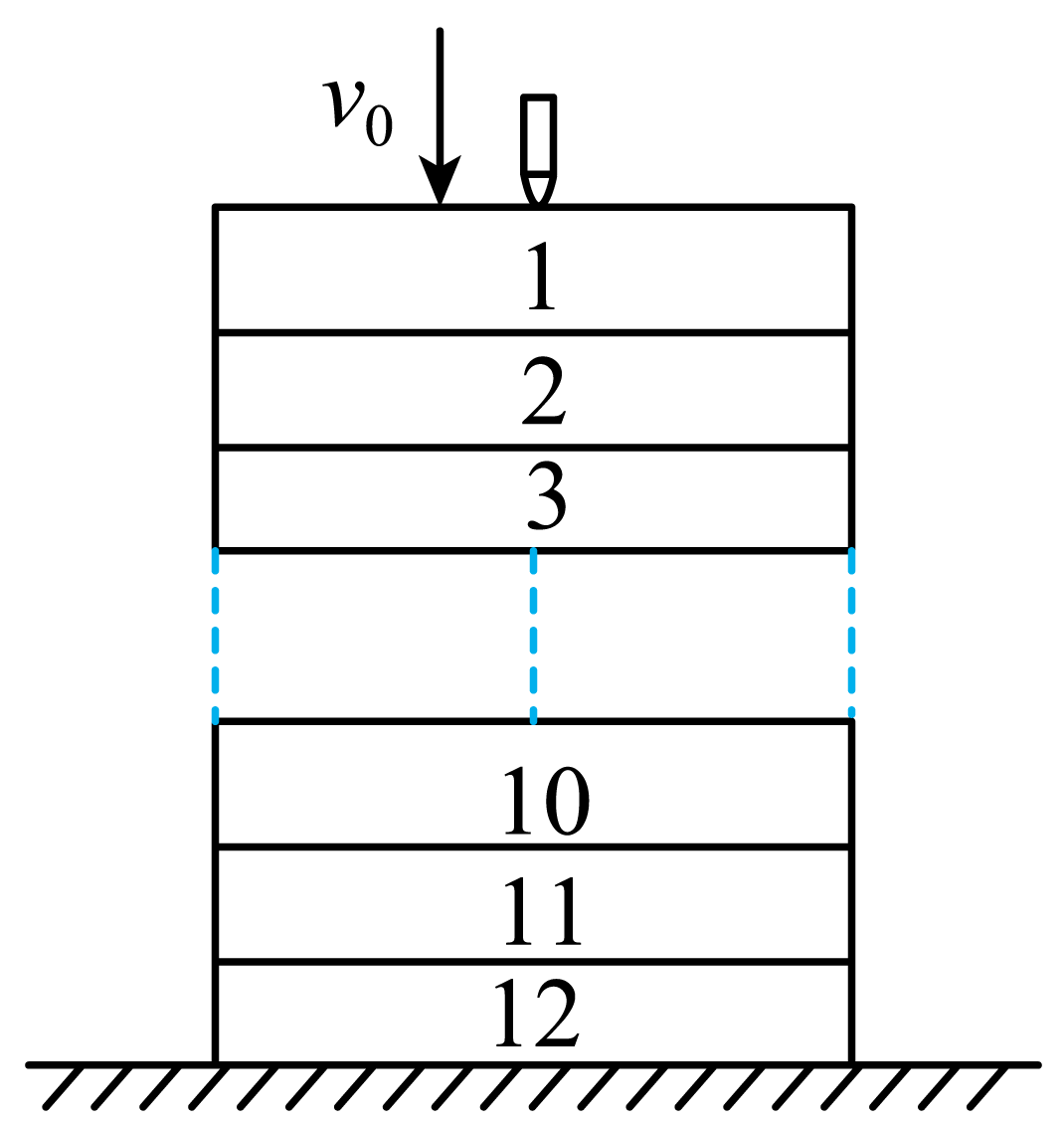
如图所示，可视为质点的子弹以初速度$v_{0}$垂直射入叠在一起的相同木板中，木板的厚度均为$d$，子弹恰好穿过第$11$块木板，已知子弹在木板中运动的总时间为$T$，且在各块木板中运动的加速度都相同。关于该子弹的运动，下列说法正确的是$(\qquad)$

运动的加速度大小为$\\dfrac{24d}{T^{2}}$

初速度为$\\dfrac{20d}{T}$

穿过第$10$块所用时间为$\\dfrac{1}{11}T$

穿过第$10$块的平均速度为$\\dfrac{\\left( \\sqrt{22}+\\sqrt{11} \\right)d}{T}$

$\rm AB$．子弹恰好穿过第$11$块木板，根据逆向思维有$11d=\dfrac{1}{2}aT^{2}$，$11d=\dfrac{v_{0}}{2}T$

解得$a=\dfrac{22d}{T^{2}}$，$v_{0}=\dfrac{22d}{T}$，选项$\rm AB$错误；

$\rm C$．设穿过前$10$块所用时间为$t_{10}$，有$10d=v_{0}t_{10}-\dfrac{1}{2}at_{10}^{2}$

解得$t_{10}=\dfrac{11-\sqrt{11}}{11}T$

设穿过前$9$块所用时间为$t_{9}$，有$9d=v_{0}t_{9}-\dfrac{1}{2}at_{9}^{2}$

解得$t_{9}=\dfrac{11-\sqrt{22}}{11}T$

穿过第$10$块所用时间$\Delta t_{10}=t_{10}-t_{9}=\dfrac{\sqrt{22}-\sqrt{11}}{11}T$，$\rm C$错误；

$\rm D$．穿过第$10$块的平均速度$\overline{v}=\dfrac{d}{\Delta t_{10}}=\dfrac{\left( \sqrt{22}+\sqrt{11} \right)d}{T}$，$\rm D$正确。

故选：$\rm D$。