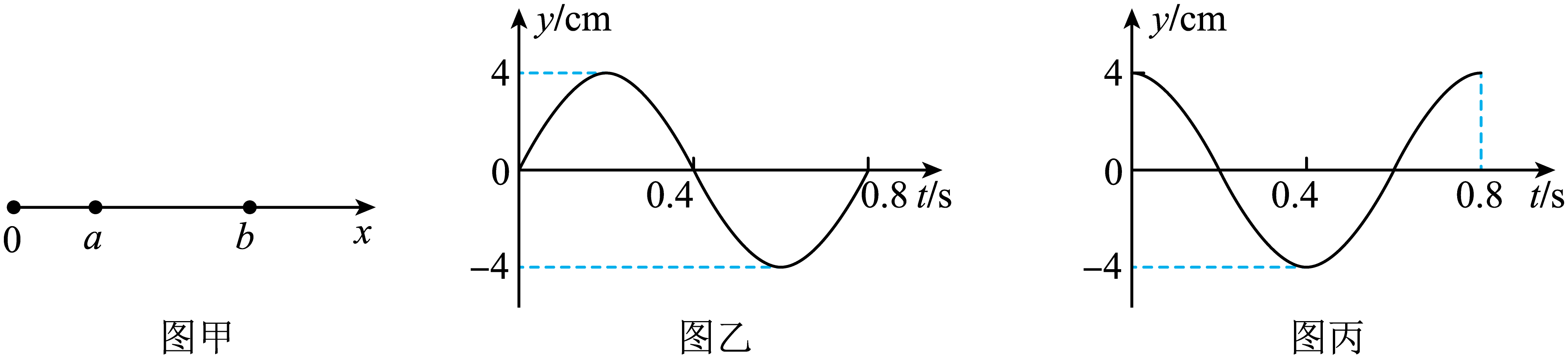
当该波在该介质中传播的速度为$5\ {\text{m}}/{\text{s}}$时，该波的波长$\lambda$；

$\\lambda=4\\;\\rm m$；

根据振动图像可得周期为$T=0.8\;\rm s$，根据波速公式有$v=\dfrac{\lambda}{T}$

代入数据，解得$\lambda=4\;\rm m$

经过$t=2\;\rm s$时间内$a$质点运动的路程$s$；

$s=40\\;\\rm cm$；

由题意，可知$t=2\;{\rm s}=2.5T$

所以质点$a$运动的路程为$s=10A=40\;\rm cm$

若该波的波长大于$0.7\;\rm m$，可能的波速$v$。

$v=\\dfrac{5}{3}\\ \\text{m/s}$；$v=5\\;\\rm \\text{m/s}$；$v= 1\\;\\rm \\text{m/s}$

如果波向右传播，则有$1\;\text{m}=\left( n+\dfrac{3}{4} \right)\lambda(n=0,1,2\cdots\cdots)$

而由于$\lambda\gt 0.7\;\rm m$，可得$n=0$

所以$\lambda_{1}=\dfrac{4}{3}\text{m}$

代入公式$v=\dfrac{\lambda}{T}$，可得$v_{1}=\dfrac{5}{3}\text{m/s}$

如果波向左传播，则有$1\;\text{m}=\left( n+\dfrac{1}{4} \right)\lambda(n=0,1,2\cdots\cdots)$

而由于$\lambda\gt 0.7\;\rm m$，可得$n=0或者n=1$

当$n=0$时，有$\lambda_{2}=4\;\rm m$，代入公式$v=\dfrac{\lambda}{T}$，可得$v_{2}=5\;\rm m/s$

当$n=1$时，有$\lambda_{3}=0.8\;\rm m$，代入公式$v=\dfrac{\lambda}{T}$，可得$v_{3}=1\;\rm m/s$