$^{13}\text{C}-\text{NMR}$能测定含碳化合物的骨架结构。在基态$^{13}\text{C}$原子中，核外存在                对自旋相反的电子。

$\\rm 2$

基态$^{13}\text{C}$原子核外有$\rm 6$个电子，电子排布式为$\rm 1s^{2}2s^{2}2p^{2}$，核外存在$\rm 2$对自旋相反的电子；

我国科学家利用$\text{CC}{{\text{l}}_{4}}$与$\text{Na}$、$\text{Mg}$等活泼金属反应合成了金刚石，为金刚石的合成提供了重要的研究思路。

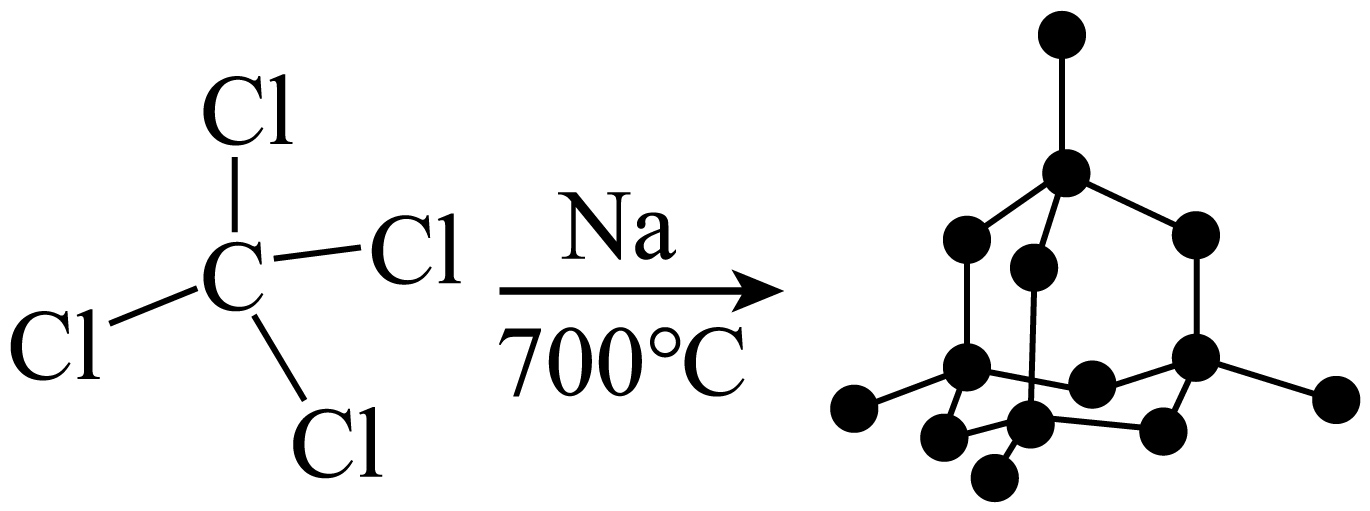
①$\text{Cl}$、$\text{Na}$、$\text{Mg}$第一电离能由大到小的顺序为                。

②$\text{CC}{{\text{l}}_{4}}$的$\text{C}-\text{Cl}$键是由碳的                轨道与氯的$\text{3p}$轨道重叠形成$\sigma$键。

$\\text{Cl}\\gt \\text{Mg}\\gt \\text{Na}$；$\\rm 1$个$\\text{s}{{\\text{p}}^{3}}$杂化

①同周期从左到右第一电离能有增大趋势，故第一电离能$\rm Cl\gt Mg\gt Na$；

②$\rm CCl_{4}$的中心原子为$\rm C$，价层电子对数为$\rm 4+\dfrac{4-4\times 1}{2}=4$，孤电子对为$\rm 0$，杂化方式为$\rm sp^{3}$杂化，$\rm C- Cl$键是由碳的$\rm 1$个$\rm sp^{3}$杂化轨道与氯的$\rm 3p$轨道重叠形成$\rm \sigma$键；

早期以石墨为原料在高温高压条件下合成金刚石。图$\rm a$为金刚石晶胞，图$\rm b$为石墨的层状结构$\rm ($虚线所示部分为其晶胞，如图$\rm c$所示$\rm )$。

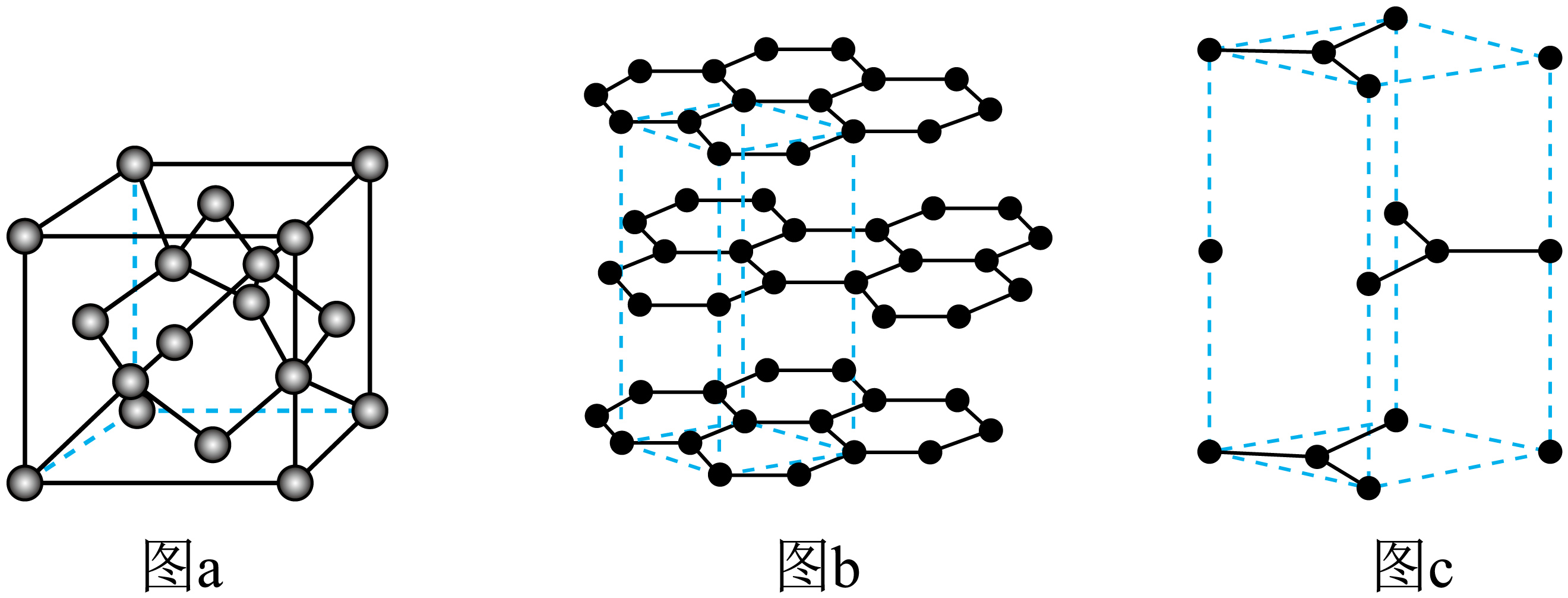
①石墨晶胞所含碳原子数为                。

②金刚石的密度为$\rho\;\rm { g}/{c}{{{m}}^{3}}$，晶胞形状为立方体，边长为${a\;\rm nm}\left( 1\;\rm {nm}={{10}^{-7}}\;\rm {cm} \right)$，阿伏加德罗常数的值为                $\rm ($用含$\rho$，${ a}$的关系式表示$\rm )$。

$\\rm 4$ $\\dfrac{96}{\\rho\\cdot {{\\left( {a}\\times {{10}^{-7}} \\right)}^{3}}}$

①图$c$为石墨的晶胞，内部有$\rm 1$个$\rm C$原子，面上有$\rm 2$个$\rm C$原子，棱上有$\rm 4$个$\rm C$原子，顶角有$\rm 8$个$\rm C$原子，$\rm C$原子个数为$\rm 1+2\times \dfrac{1}{2}+4\times \dfrac{1}{6}+4\times \dfrac{1}{12}+2\times \dfrac{1}{3}+2\times \dfrac{1}{6}=4$；

②金刚石晶胞中$\rm C$原子数为$\rm 4+8\times \dfrac{1}{8}\rm +6\times \dfrac{1}{2}\rm =8$，质量为$\dfrac{8\times 12}{{{{N}}_{\rm {A}}}}\rm \;{g}$，体积为$ (a\times 10^{-7})^{3}\;\rm cm^{3}$，根据密度公式$\rho=\dfrac{{m}}{{V}}=\dfrac{\dfrac{8\times 12}{{{{N}}_{\rm {A}}}}}{{{({a}\times {{10}^{-7}})}^{3}}}$，$ N_{\rm A}=\dfrac{96}{\rho\cdot {{\left( {a}\times {{10}^{-7}} \right)}^{3}}}$；

碳在物质转化中起着重要作用。$\text{Si}{{\text{O}}_{2}}$与$\text{C}{{\text{l}}_{2}}$较难发生反应：$\text{Si}{{\text{O}}_{2}}(\text{s})+2\text{C}{{\text{l}}_{2}}(\text{g})=\text{SiC}{{\text{l}}_{4}}(\text{g})+{{\text{O}}_{2}}(\text{g})\qquad \Delta {H}\gt 0$，加碳生成$\text{CO}$可使反应得以进行。解释加碳反应更易进行的原因：                。

$\\rm C$和${{\\text{O}}_{2}}$生成$\\text{CO}$并放热，使$\\text{Si}{{\\text{O}}_{2}}+2\\text{C}{{\\text{l}}_{2}}+2\\text{C}=\\text{SiC}{{\\text{l}}_{6}}+2\\text{CO}$反应趋势变大$\\rm ($碳与${{\\text{O}}_{2}}$反应生成$\\text{CO}$放出热量，使体系温度升高，同时降低$ {c}\\left( {{\\text{O}}_{2}} \\right)$，均促进反应正向进行$\\rm )$

$\text{Si}{{\text{O}}_{2}}(\text{s})+2\text{C}{{\text{l}}_{2}}(\text{g})=\text{SiC}{{\text{l}}_{4}}(\text{g})+{{\text{O}}_{2}}(\text{g})\qquad \Delta {H}\gt 0$，$\Delta S\lt 0$，反应难以自发进行，加碳生成$\rm CO$，放出热量，使温度升高，总反应$\text{Si}{{\text{O}}_{2}}+2\text{C}{{\text{l}}_{2}}+2\text{C}=\text{SiC}{{\text{l}}_{6}}+2\text{CO}$趋势变大，同时消耗了$\rm O_{2}$，使平衡正向进行。