$\rm Cu$在元素周期表中位于第                周期第                族；基态$\text{C}{{\text{u}}^{2+}}$核外有                个未成对电子。

四 ； $\\rm IB$ ； $\\rm 1$

$\rm Cu$为$\rm 29$号元素，在元素周期表中位于第四周期第$\rm IB$族；基态$\rm Cu$原子的价电子排布式为$3{{\text{d}}^{10}}4{{\text{s}}^{1}}$，基态$\text{C}{{\text{u}}^{2+}}$的价电子排布式为$3{{\text{d}}^{9}}$，则基态$\text{C}{{\text{u}}^{2+}}$核外有$\rm 1$个未成对电子。

蓝矾的简单结构如图$\rm 1$。

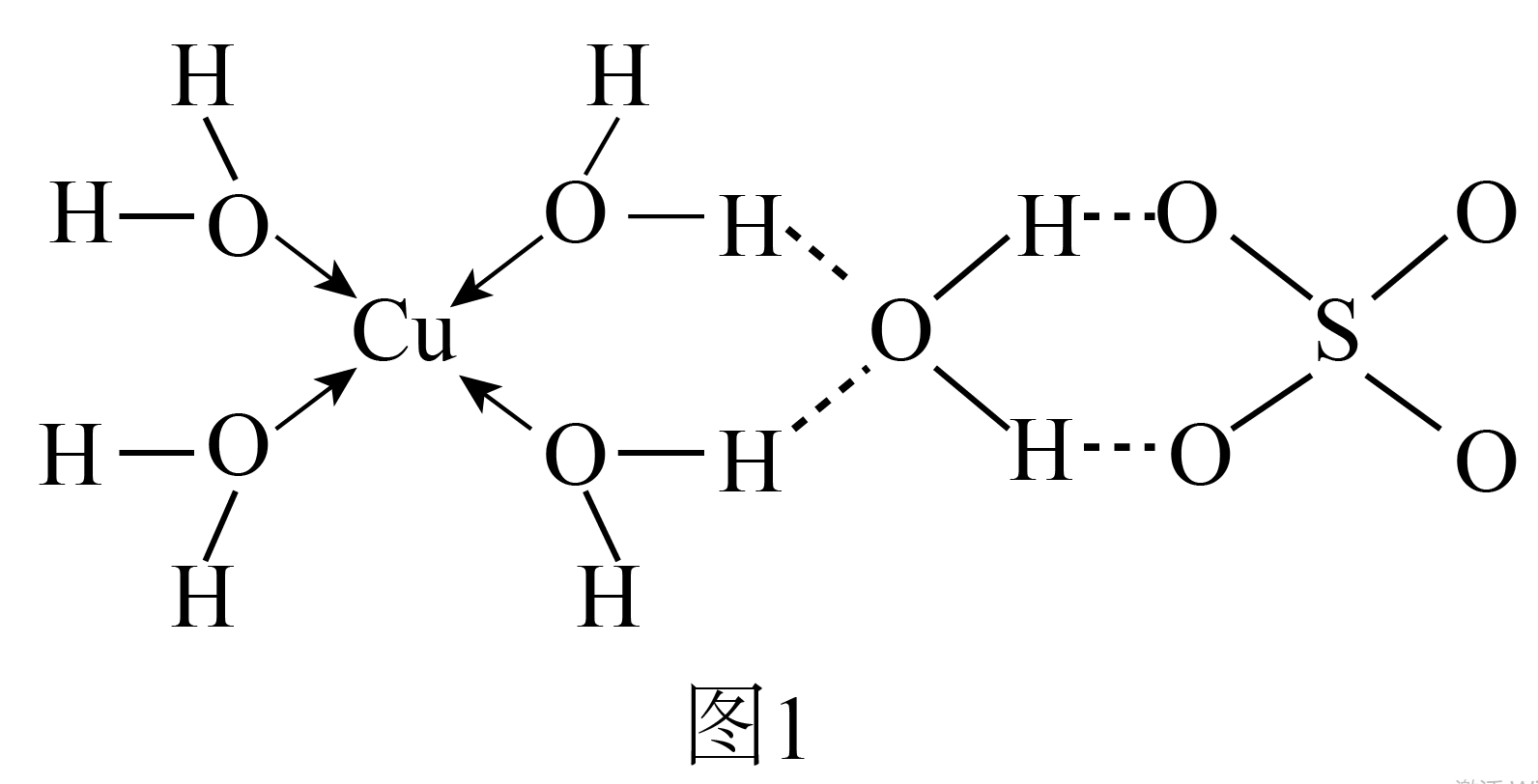
蓝矾晶体中形成配位键时                提供空轨道。$\text{SO}_{4}^{2-}$的空间结构为                。蓝矾晶体中形成配位键的${{\text{H}}_{2}}\text{O}$分子的$\rm H-O-H$键角                $\rm ($填“$\rm \gt $”“$\rm =$”或“$\rm \lt $”$\rm )104.5^\circ$。

$\\text{C}{{\\text{u}}^{2+}}$ ； 正四面体 ； $\\rm \\gt $

由蓝矾的结构可知，其晶体可表示为$\left[ \text{Cu}{{\left( {{\text{H}}_{2}}\text{O} \right)}_{4}} \right]\text{S}{{\text{O}}_{4}}\cdot {{\text{H}}_{2}}\text{O}$，晶体中含$\text{Cu}-\text{O}$配位键，其中$\rm O$提供孤电子对，$\text{C}{{\text{u}}^{2+}}$提供空轨道。$\text{SO}_{4}^{2-}$的中心原子$\rm S$的$\rm \sigma$键为$\rm 4$，孤电子对数为$\dfrac{6+2-2\times 4}{2}=0$，中心$\rm S$原子采取$\text{s}{{\text{p}}^{3}}$杂化，$\text{SO}_{4}^{2-}$的空间结构为正四面体。水分子中的$\text{H}-\text{O}-\text{H}$键角为${{104.5}^{{}^\circ }}$，蓝矾晶体中形成配位键的水分子的孤电子对参与成键，成键电子对之间的斥力小于水中孤电子对对成键电子对的斥力，蓝矾晶体中形成配位键的${{\text{H}}_{2}}\text{O}$分子的$\rm H-O-H$键角大于$\rm 104.5^\circ$。

二维导电金属$\rm -$有机框架$\rm (MOFs)$因其在超级电容器、电化学传感器、电催化剂和电池等方面的潜在应用而受到越来越多的关注。合成$\rm MOFs$的一种方法如下。

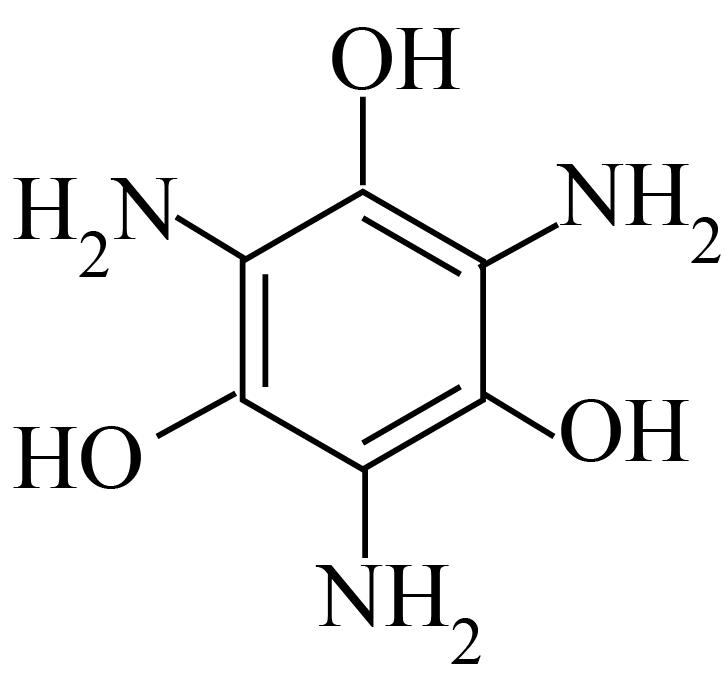$\cdot 3\text{HCl}+\text{Cu}{{\left( \text{N}{{\text{O}}_{3}} \right)}_{2}}\cdot 3{{\text{H}}_{2}}\text{O}$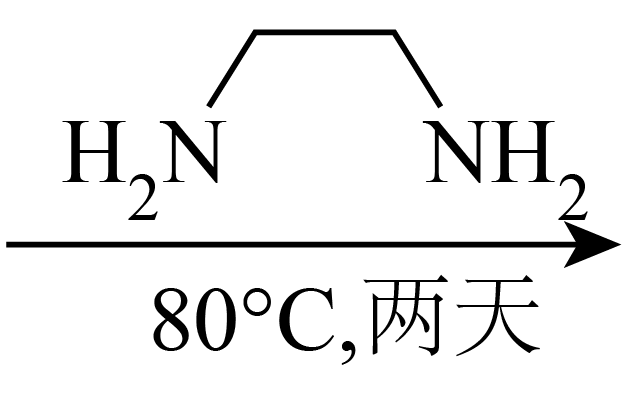$\rm MOFs$

固态$\cdot 3\text{HCl}$的晶体类型是                。中$\rm N$原子的杂化方式是                。

离子晶体 ； $\\text{s}{{\\text{p}}^{3}}$

$\cdot\!\!\text{ 3HCl}$类似于$\text{N}{{\text{H}}_{4}}\text{Cl}$，属于离子晶体。${{\text{H}}_{2}}\text{NC}{{\text{H}}_{2}}\text{C}{{\text{H}}_{2}}\text{N}{{\text{H}}_{2}}$分子的氨基中$\rm N$原子为$\text{s}{{\text{p}}^{3}}$杂化。

一种含铜的多元金属硫化物的晶胞结构为四方晶系，已知金属原子均呈四面体配位，晶胞棱边夹角均为$\rm 90^\circ$，其结构可看作是由两个立方体$\rm A$、$\rm B$上下堆叠而成。图$\rm 2$为$\rm A$沿体对角线的投影图，图$\rm 3$为$\rm B$沿$y$轴方向的投影图。$\rm A$中$\rm Fe$、$\rm Sn$位置互换即为  $\rm B$．立方体$\rm A$、$\rm B$棱长均为$a\text{ pm}$，晶胞中部分原子的分数坐标为$\rm S(0$，$\rm 0$，$\rm 0)$、$\rm Fe\left( \dfrac{3}{4},\dfrac{1}{4},\dfrac{1}{8} \right)$。

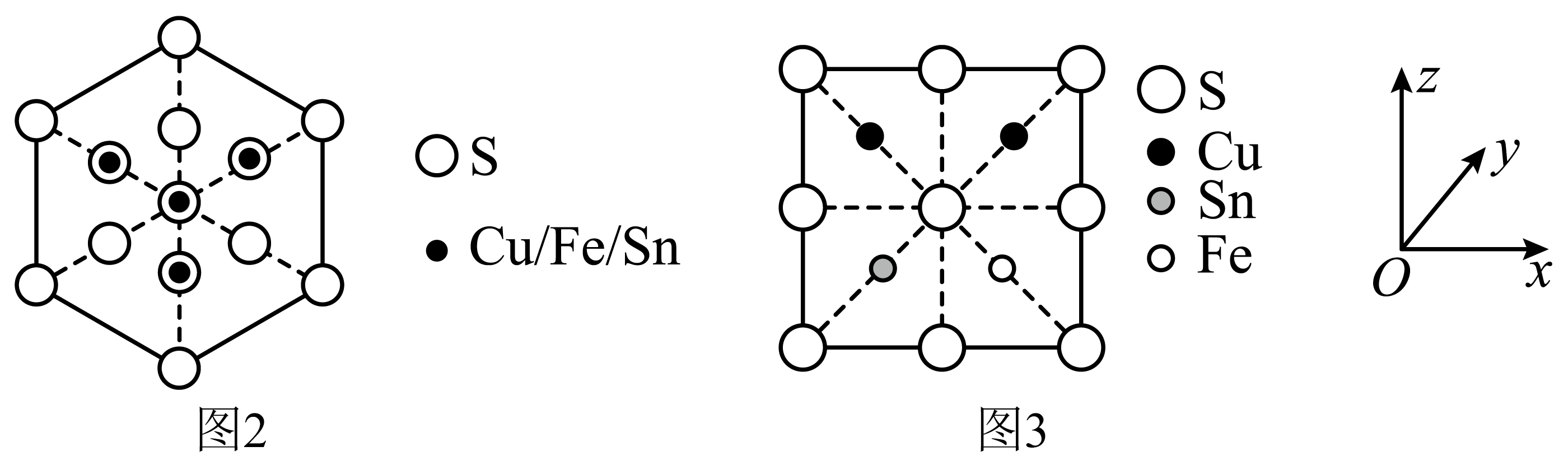
晶胞中$\rm Sn$原子的分数坐标为                。若该晶体的密度为$d\,\text{g}\cdot \text{c}{{\text{m}}^{-3}}$，则阿伏加德罗常数${{{N}}_{\text{A}}}=$                。

$\\left( \\dfrac{1}{4},\\dfrac{3}{4},\\dfrac{1}{8} \\right)$，$\\left( \\dfrac{3}{4},\\dfrac{1}{4},\\dfrac{5}{8} \\right)$ ； $\\dfrac{4.31 \\times 10^{32}}{a^3 d} \\mathrm{ mol}^{-1}$

根据题意分析该晶体采用面心立方最密堆积，$\rm S$原子位于立方体$\rm A$、$\rm B$的顶点和面心，$\text{Cu}$、$\text{Fe}$、$\text{Sn}$位于体内，$\rm 1$个晶胞中含$\rm S$原子个数为$8\times \dfrac{1}{8}+10\times \dfrac{1}{2}+4\times \dfrac{1}{4}+1=8$，$\text{Cu}$原子个数为$\rm 4$，$\text{Fe}$原子个数为$\rm 2$，$\rm Sn$原子个数为$\rm 2$，因此该晶体的化学式为$\text{C}{{\text{u}}_{2}}\text{FeSn}{{\text{S}}_{4}}$，$\rm B$在下面，根据图$\rm 3$可以确定$\rm B$中$\rm Sn$原子的分数坐标为$\left( \dfrac{1}{4},\dfrac{3}{4},\dfrac{1}{8} \right)$，则$\rm A$中$\rm Sn$原子的分数坐标为$\left( \dfrac{3}{4},\dfrac{1}{4},\dfrac{5}{8} \right)$，晶体的密度$d=\dfrac{\left( 64\times 4+56\times 2+119\times 2+32\times 8 \right)\,\,\text{g}\cdot \text{mo}{{\text{l}}^{-1}}}{{{N}_{\text{A}}}\times 2{{a}^{3}}\times {{10}^{-30}}\,\,\text{c}{{\text{m}}^{-3}}}$，则${{N}_{\text{A}}}=\dfrac{4.31\times {{10}^{32}}}{{{a}^{3}}d}\,\text{mo}{{\text{l}}^{-1}}$。