$400\text{ }{}^\circ \text{C}$时将$\text{CO}(\text{g})$和${{\text{H}}_{2}}\text{O}(\text{g})$各$\text{0}.\text{1}\,\text{mol}$通入容积为$\text{2 L}$的密闭容器中仅发生反应$2$，$8\,\text{min}$时$\text{CO}$的转化率是$40\%$，用${{\text{H}}_{2}}$的浓度变化表示的反应速率$v\left( {{\text{H}}_{2}} \right)=$                $\text{mol}\cdot {{\text{L}}^{-1}}\cdot \text{mi}{{\text{n}}^{-1}}$。

$\\rm 0.0025$

$400\text{ }{}^\circ \text{C}$时将$\text{CO}(\text{g})$和${{\text{H}}_{2}}\text{O}(\text{g})$各$\text{0}.\text{1}\,\text{mol}$通入容积为$\text{2 L}$的密闭容器中仅发生反应$2$，$8\,\text{min}$时$\text{CO}$的转化率是$40\%$，列出三段式：

$\begin{matrix} {} & \text{CO}(\text{g}) & + & {{\text{H}}_{2}}\text{O}(\text{g}) & \rightleftharpoons & \text{C}{{\text{O}}_{2}}(\text{g}) & + & {{\text{H}}_{2}}(\text{g}) \\起始 (\text{mol}) & 0.1 & {} & 0.1 & {} & 0 & {} & 0 \\转化 (\text{mol}) & 0.04 & {} & 0.04 & {} & 0.04 & {} & 0.04 \\ 平衡(\text{mol}) & 0.06 & {} & 0.06 & {} & 0.04 & {} & 0.04 \\ \end{matrix}$

用${{\text{H}}_{2}}$的浓度变化表示的反应速率$v\left( {{\text{H}}_{2}} \right)=\dfrac{0.04\,\text{mol}}{2\,\text{L}\times 8\,\min }=0.0025\,\text{mol}\cdot {{\text{L}}^{-1}}\cdot \text{mi}{{\text{n}}^{-1}}$。

恒温恒压时向体系中充入一定量${{\text{N}}_{2}}\rm ($不参与反应$\rm )$可提高${{\text{H}}_{2}}$的平衡产率，原因为                。

反应$\\rm 1$为气体分子数增大的反应，恒温恒压时向体系中充入一定量$\\rm N_{2}$，相当于减压，降低各气体分压$\\rm ($相当于扩大容器体积$\\rm )$，会使反应$\\rm 1$的平衡正向移动

反应$\rm 1$为气体分子数增大的反应，恒温恒压时向体系中充入一定量$\rm N_{2}$，相当于减压，降低各气体分压$\rm ($相当于扩大容器体积$\rm )$，会使反应$\rm 1$的平衡正向移动，所以充入一定量${{\text{N}}_{2}}\rm ($不参与反应$\rm )$可提高${{\text{H}}_{2}}$的平衡产率。

Ⅱ$\rm .$乙醇与水催化反应制氢气

发生以下三个反应：

反应$\rm 3$：${{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}(\text{g})+{{\text{H}}_{2}}\text{O}(\text{g})\rightleftharpoons 2\text{CO}(\text{g})+4{{\text{H}}_{2}}(\text{g})\quad \Delta {{H}_{1}}=+255.7\,\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$  

反应$\rm 4$：$\text{CO}(\text{g})+{{\text{H}}_{2}}\text{O}(\text{g})\rightleftharpoons \text{C}{{\text{O}}_{2}}(\text{g})+{{\text{H}}_{2}}(\text{g})\quad \Delta {{H}_{2}}=-41.35\,\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$  

反应$\rm 5$：${{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}(\text{g})+3{{\text{H}}_{2}}\text{O}(\text{g})\rightleftharpoons 2\text{C}{{\text{O}}_{2}}(\text{g})+6{{\text{H}}_{2}}(\text{g})\quad \Delta {{H}_{3}}$  

计算$\Delta {{H}_{3}}=$                $\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$。

$\\rm 173$

反应$\rm 3$：${{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}(\text{g})+{{\text{H}}_{2}}\text{O}(\text{g})\rightleftharpoons 2\text{CO}(\text{g})+4{{\text{H}}_{2}}(\text{g})\quad \Delta {{H}_{1}}=+255.7\,\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

反应$\rm 4$：$\text{CO}(\text{g})+{{\text{H}}_{2}}\text{O}(\text{g})\rightleftharpoons \text{C}{{\text{O}}_{2}}(\text{g})+{{\text{H}}_{2}}(\text{g})\quad \Delta {{H}_{2}}=-41.35\,\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

反应$\rm 5$：${{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}(\text{g})+3{{\text{H}}_{2}}\text{O}(\text{g})\rightleftharpoons 2\text{C}{{\text{O}}_{2}}(\text{g})+6{{\text{H}}_{2}}(\text{g})\quad \Delta {{H}_{3}}$

由盖斯定律反应$\rm 5=$反应$\rm 3+2\times $反应$\rm 4$，则$\Delta {{H}_{\text{3}}}\text{=(}+255.7\,\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}})+2\times (-41.35\,\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}})=173\,\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$。

恒容条件下，将$2\text{ mol }{{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}(\text{g})$和$6\text{ mol }{{\text{H}}_{2}}\text{O}(\text{g})$投入密闭容器中发生Ⅱ中三个反应，平衡时$\text{C}{{\text{O}}_{2}}$和$\text{CO}$的选择性以及乙醇的转化率随温度的变化曲线如图所示。

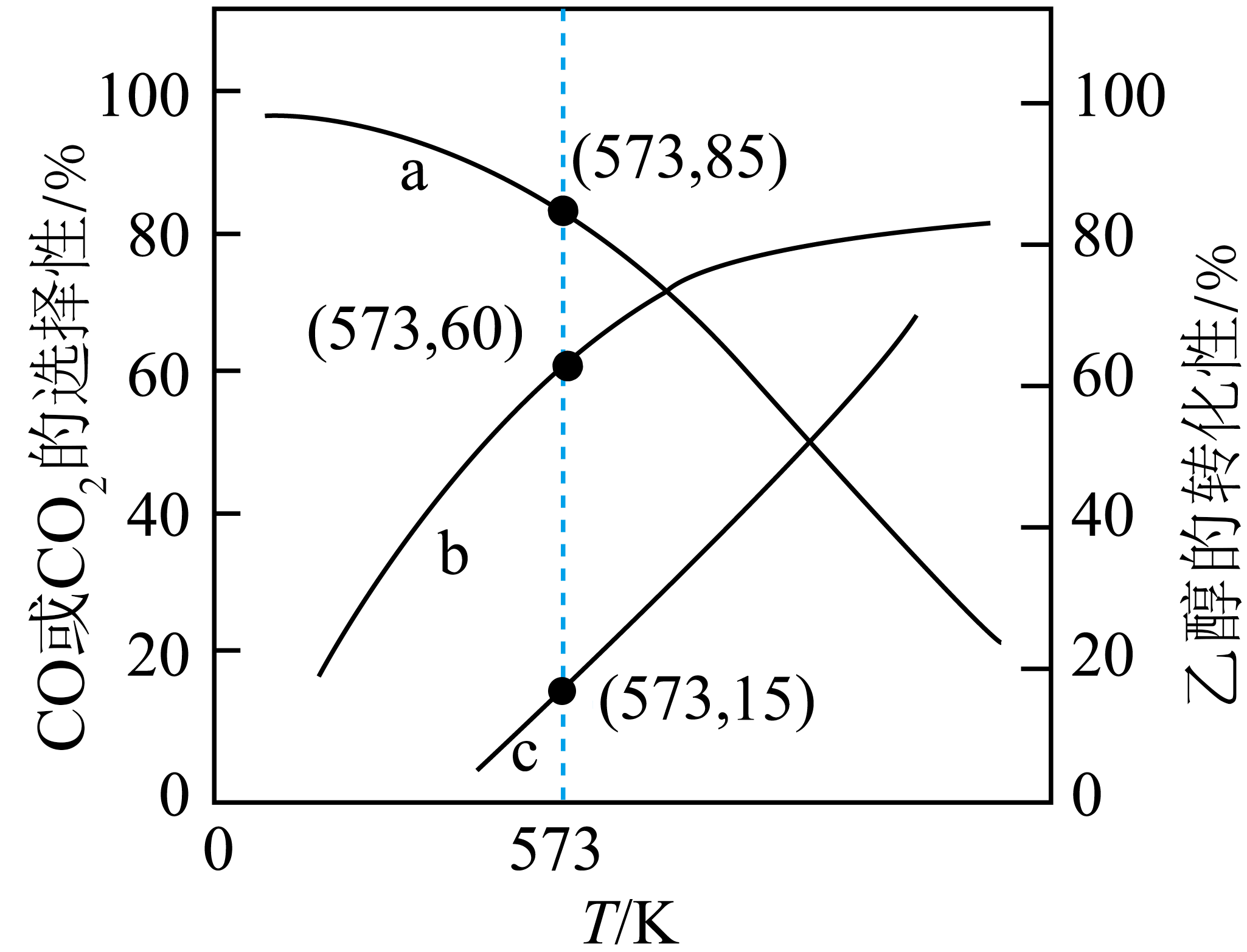
已知：$\text{CO}$的选择性$=\dfrac{{{n}_{生成}}(\text{CO})}{2{{n}_{反应}}\left( {{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH} \right)}\times 100\%$

①表示$\text{CO}$选择性的曲线是                $\rm ($填“$\text{a}$”“$\text{b}$”或“$\text{c}$”$\rm )$。

②$\text{573 K}$时，反应$\rm 4$的压强平衡常数${{K}_{\text{p}}}=$                $\rm ($已知：分压$=$总压$\times $该组分物质的量分数，计算结果保留整数$\rm )$。

$\\rm c$ ； $\\rm 14$

①反应$\rm 3$、$\rm 5$为吸热反应，反应$\rm 4$为放热反应，随着温度的升高，反应$\rm 3$、$\rm 5$平衡正向移动，反应$\rm 4$平衡逆向移动，反应$\rm 4$逆向移动$\rm CO_{2}$转化为$\rm CO$，故温度升高$\rm CO$的选择性增大，$\rm CO_{2}$的选择性减小。表示$\rm CO_{2}$选择性的曲线为$\rm a$，表示$\rm CO$选择性的曲线为$\rm c($同温度下两条选择性曲线上的点的和为$\rm 100\%)$，表示$\rm C_{2}H_{5}OH$转化率的曲线是$\rm b$；

②$\rm CO$的选择性$\rm +CO_{2}$的选择性$\rm =1$，乙醇与水的投料分别为$\rm 2$ $\rm mol$和$\rm 6$ $\rm mol$，$\text{573 K}$时，$\rm CO$的选择性为$\rm 15\%$，$\rm CO_{2}$的选择性为$\rm 85\%$，则$n\left( \text{C}{{\text{O}}_{\text{2}}} \right)n\left( \text{CO} \right)=0.85:0.15$，乙醇的转化率为$\rm 60\%$，列出三段式：

$\begin{matrix} {} & {{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}\left( \text{g} \right) & + & {{\text{H}}_{2}}\text{O}\left( \text{g} \right) & \rightleftharpoons & 2\text{CO}\left( \text{g} \right) & + & 4{{\text{H}}_{2}}\left( \text{g} \right) \\起始 \left( \text{mol} \right) & 2 & {} & 6 & {} & 0 & {} & 0 \\转化 \left( \text{mol} \right) & x & {} & x & {} & 2x & {} & 4x \\平衡 \left( \text{mol} \right) & 2-x & {} & 6-x & {} & 2x & {} & 4x \\ \end{matrix}$

设反应$\rm 4$转化${\rm CO}\ { }y\ \text{ mol}$，

$\begin{matrix} {} & \text{CO}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) & \rightleftharpoons & \text{C}{{\text{O}}_{\text{2}}}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\left( \text{g} \right) \\起始 \left( \text{mol} \right) & 2x & {} & 6-x & {} & 0 & {} & 4x \\ 转化\left( \text{mol} \right) & y & {} & y & {} & y & {} & y \\平衡 \left( \text{mol} \right) & 2x-y & {} & 6-x-y & {} & y & {} & 4x+y \\ \end{matrix}$

因乙醇的转化率为$\rm 60\%$，则反应$\rm 5$转化乙醇为$1.2-x$，

$\begin{matrix} {} & {{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}\left( \text{g} \right) & + & 3{{\text{H}}_{2}}\text{O}\left( \text{g} \right) & \rightleftharpoons & 2\text{C}{{\text{O}}_{2}}\left( \text{g} \right) & + & 6{{\text{H}}_{2}}\left( \text{g} \right) \\ 起始\left( \text{mol} \right) & 2-x & {} & 6-x-y & {} & y & {} & 4x+y \\ 转化\left( \text{mol} \right) & 1.2-x & {} & 3.6-3x & {} & 2.4-2x & {} & 7.2-6x \\平衡 \left( \text{mol} \right) & 0.8 & {} & 2.4+2x-y & {} & 2.4-2x+y & {} & 7.2-2x+y \\ \end{matrix}$

$\rm CO$的物质的量为$\rm 1.2$ $\rm mol\times 15\%\times 2=0.36$ $\rm mol$，则$2x-y=0.36$，则$n\left( {{\text{H}}_{\text{2}}}\text{O} \right)=2.76\,\text{mol}$，$n\left( {{\text{H}}_{\text{2}}} \right)=6.84\,\text{mol}$，$n\left( {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{OH} \right)=0.8\,\text{mol}$，$n\left( \text{CO} \right)=0.36\,\text{mol}$，$n\left( \text{C}{{\text{O}}_{\text{2}}} \right)=2.04\,\text{mol}$，总物质的量为$\rm 12.8$ $\rm mol$，该反应各物质系数均为$\rm 1$，分压压强之比等于物质的量之比，反应$\rm 4$的压强平衡常数${{K}_{\text{p}}}=\dfrac{p\left( {{\text{H}}_{2}} \right)p\left( \text{C}{{\text{O}}_{2}} \right)}{p\left( \text{CO} \right)p\left( {{\text{H}}_{2}}\text{O} \right)}=\dfrac{6.84\times 2.04}{0.36\times 2.76}\approx 14$。

Ⅲ$\rm .$化工燃料重整制氢

反应为：$\text{C}{{\text{H}}_{4}}(\text{g})+\text{C}{{\text{O}}_{2}}(\text{g})\rightleftharpoons 2\text{CO}(\text{g})+2{{\text{H}}_{2}}(\text{g})$

$900\text{ }{}^\circ \text{C}$，将$\text{C}{{\text{H}}_{4}}$和$\text{C}{{\text{O}}_{2}}$的混合气体$\rm ($投料比$1:1\rm )$按一定流速通过盛有炭催化剂的反应器，测得$\text{C}{{\text{H}}_{4}}$的转化率受炭催化剂颗粒大小的影响如图所示$\rm ($注：目数越大，表示炭催化剂颗粒越小$\rm )$。

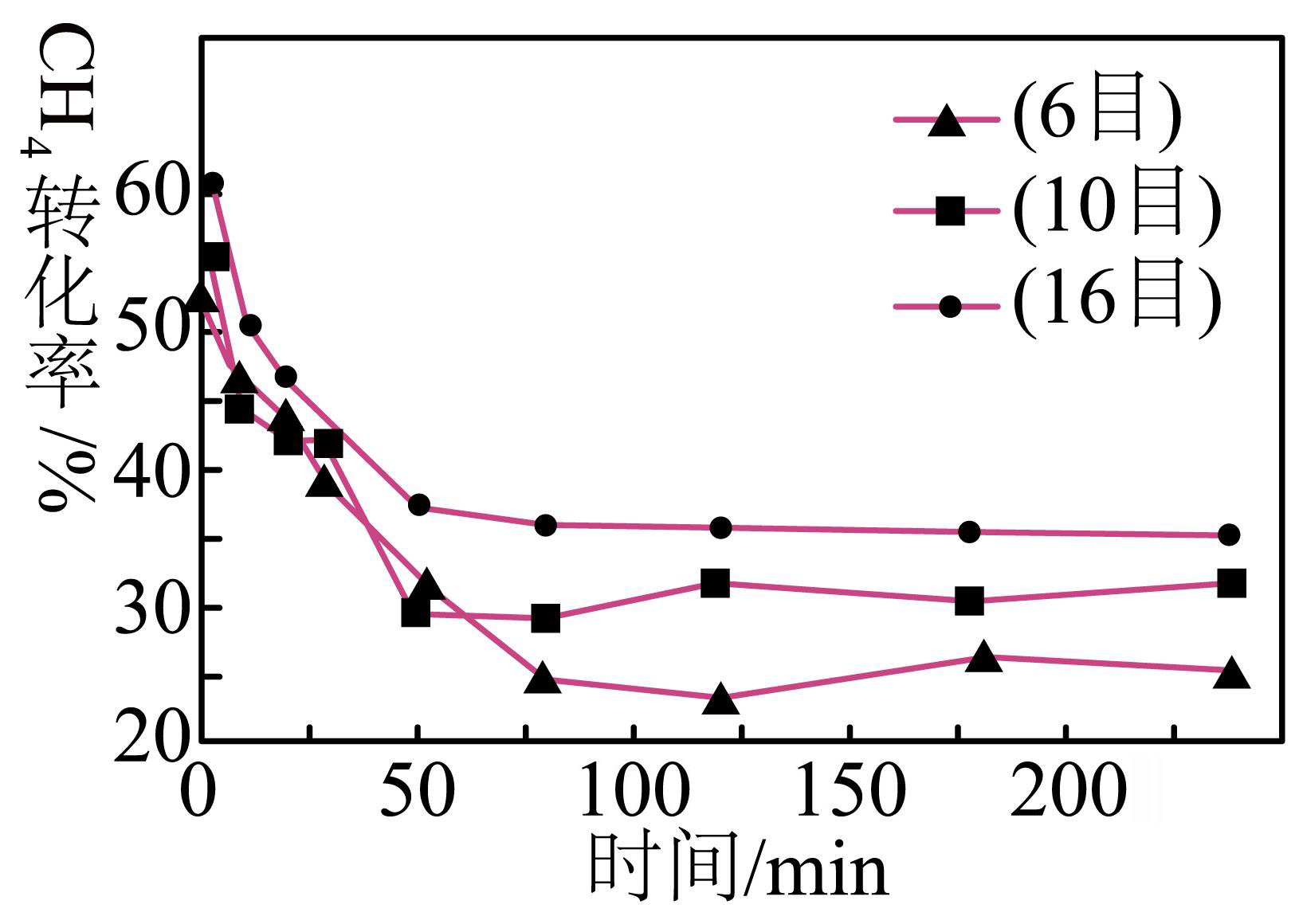
由图可知，$\text{70}\,\text{min}$后$\text{C}{{\text{H}}_{4}}$的转化率与炭催化剂的目数的关系为                ，原因是                。

达到化学平衡前，催化剂目数越大，反应速率越快，在相同时间反应的甲烷更多，$\\rm CH_{4}$转化率越大 ； 催化剂目数越大，颗粒越小，表面积越大，原料气与催化剂的接触更加充分，反应更完全

据图可知，$\rm 70$ $\rm min$后在反应达到化学平衡前，催化剂目数越大，反应速率越快，在相同时间反应的甲烷更多，$\rm CH_{4}$转化率越大，因为催化剂目数越大，颗粒越小，表面积越大，原料气与催化剂的接触更加充分，反应更完全。