反应$\rm I$在                $\rm ($填“高温”“低温”“任何温度”或“任何温度都不”$\rm )$能自发进行。

任何温度

反应 $\rm I$为放热且是熵增的反应，即其$\Delta H\lt 0$，$\Delta S\lt 0$，根据$\Delta G=\Delta H-T\Delta S\lt 0$，反应可以发生，则该反应在任何温度能自发进行；

在初始压强${{p}_{0}}=100\text{ kPa}$的条件下，向某恒容密闭容器中按不同物质的量之比投入$\text{C}{{\text{H}}_{4}}、\text{C}{{\text{O}}_{2}}$和${{\text{H}}_{2}}\text{O}$，在不同温度下反应相同时间后，提到${{\text{H}}_{2}}$产率如图所示$\rm ({{\text{H}}_{2}}$产率$=\left. \dfrac{2{{n}_{生成}}\left( {{\text{H}}_{2}} \right)}{4{{n}_{投入}}\left( \text{C}{{\text{H}}_{4}} \right)+2{{n}_{投入}}\left( {{\text{H}}_{2}}\text{O} \right)} \right)$。

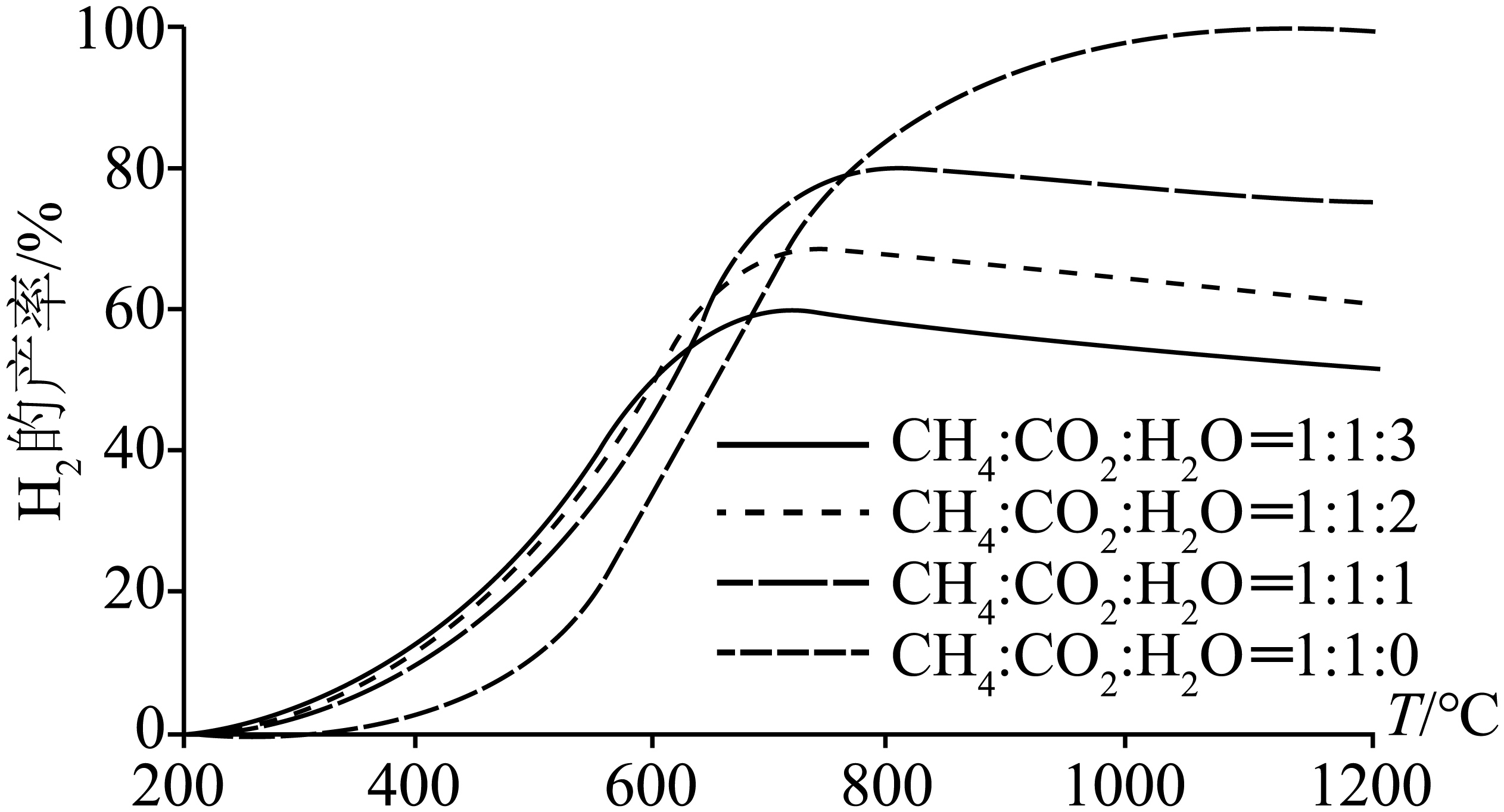
①四条曲线先升高后降低，降低的原因是                。

②由图可知，当$1000\ {}^\circ \text{C}$，$\text{C}{{\text{H}}_{4}}:\text{C}{{\text{O}}_{2}}:{{\text{H}}_{2}}\text{O}=1:1:0$时，${{\text{H}}_{2}}$产率接近$100\%$，随着${{\text{H}}_{2}}\text{O}$的投入增加，${{\text{H}}_{2}}$产率降低的原因是                

③在$\text{C}{{\text{H}}_{4}}:\text{C}{{\text{O}}_{2}}:{{\text{H}}_{2}}\text{O}=1:1:3$的条件下，已知温度为$T$时，$\text{C}{{\text{H}}_{4}}$的平衡转化率为$50\%{{\text{H}}_{2}}$的平衡产率为$26\%$，则此时容器中$\text{CO}$的分压为                $\text{kPa}\rm ($保留两位有效数字$\rm )$，反应$\rm III$的分压平衡常数${{K}_{\text{p}}}=$                $\rm ($保留两位有效数字$\rm )$。

反应体系已达平衡，反应$\\rm I$和$\\rm II$均为放热反应，温度越高平衡逆向移动 ； $1000\\ {}^\\circ \\text{C}$时，反应$\\rm I$和$\\rm II$处于平衡状态，反应$\\rm I$的程度小于反应$\\rm II$ ； $\\rm 14$ ； $\\rm 0.55$

①温度越高反应速率越快，则相同的时间内，温度较高时，反应可以达到平衡，且可以发生移动，在反应 $\rm I$ 和 $\rm II$ 中氢气是产物，平衡后平衡逆向移动，其产率会降低；

②由图可知，当 $1000\ {}^\circ \text{C}$时，该反应已经达到平衡，当水的投入量为$\rm 0$时，${{\text{H}}_{2}}$ 产率接近 $100\%$，说明此时反应 $\rm I$ 的程度小于反应$\rm II$，加入水后，反应$\rm I$开始反应，但是程度较小，根据氢气产率定义可知其产率降低；

③设$\rm CH_{4}$、$\rm CO_{2}$、$\rm H_{2}O$的物质的量分别为$x$、$x$、$3x$，设参加反应$\rm I$的甲烷的物质的量为$a$ $\rm mol$，$\text{C}{{\text{H}}_{4}}$的平衡转化率为$50\%$，${{\text{H}}_{2}}$的平衡产率为$26\%$，可得以下三段式：

$\begin{matrix} {} & \text{C}{{\text{H}}_{\text{4}}}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) & \rightleftharpoons & \text{CO}\left( \text{g} \right) & + & \text{3}{{\text{H}}_{\text{2}}}\left( \text{g} \right) \\开始 \text{(mol)} & x & {} & 3x & {} & \text{0} & {} & \text{0} \\转化 \text{(mol)} & a & {} & a & {} & a & {} & 3a \\ 平衡\text{(mol)} & x-a & {} & 3x-a & {} & a & {} & 3a \\ \end{matrix}$

$\begin{matrix} {} & \text{C}{{\text{H}}_{\text{4}}}\left( \text{g} \right) & + & \text{C}{{\text{O}}_{\text{2}}}\left( \text{g} \right) & \rightleftharpoons & \text{2CO}\left( \text{g} \right) & + & \text{2}{{\text{H}}_{\text{2}}}\left( \text{g} \right) \\开始 \text{(mol)} & x-a & {} & x & {} & a & {} & 3a \\ 转化\text{(mol)} & 0.5x-a & {} & 0.5x-a & {} & x-2a & {} & x-2a \\平衡 \text{(mol)} & 0.5x & {} & 0.5x+a & {} & x-a & {} & x+a \\ \end{matrix}$

$26\%=\dfrac{2n({{\text{H}}_{2}})}{4x+2\times 3x}$，解得$n\left( {{\text{H}}_{\text{2}}} \right)=1.3x$；

$\begin{matrix} {} & \text{CO}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) & \rightleftharpoons & \text{C}{{\text{O}}_{\text{2}}}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\left( \text{g} \right) \\开始 \text{(mol)} & x-a & {} & 3x-a & {} & 0.5x+a & {} & x+a \\ 转化\text{(mol)} & 0.3x-a & {} & 0.3x-a & {} & 0.3x-a & {} & 1.3x-(x+a)=0.3x-a \\平衡 \text{(mol)} & 0.7x & {} & 2.7x & {} & 0.8x & {} & 1.3x \\ \end{matrix}$

由于是恒容容器，则平衡时的压强，${{P}_{平}}=\dfrac{0.7x+2.7x+0.8x+1.3x+0.5x}{x+x+3x}\times 100\text{ kPa}=\dfrac{6}{5}\times 100\text{ kPa}$，

则此时容器中$\text{CO}$的分压为$\dfrac{0.7x}{0.7x+2.7x+0.8x+1.3x+0.5x}\times \dfrac{6}{5}\times 100\text{ kPa}=14\text{ kPa}$；

由于反应$\rm III$是气体分子数不变的反应，可以用物质的量来计算分压平衡常数${{K}_{\text{p}}}=\dfrac{0.8x\times 1.3x}{0.7x\times 2.7x}=0.55$；

利用电催化法将$\text{C}{{\text{O}}_{2}}$转化为$\text{C}{{\text{H}}_{3}}\text{OH}$的一种方法如图：

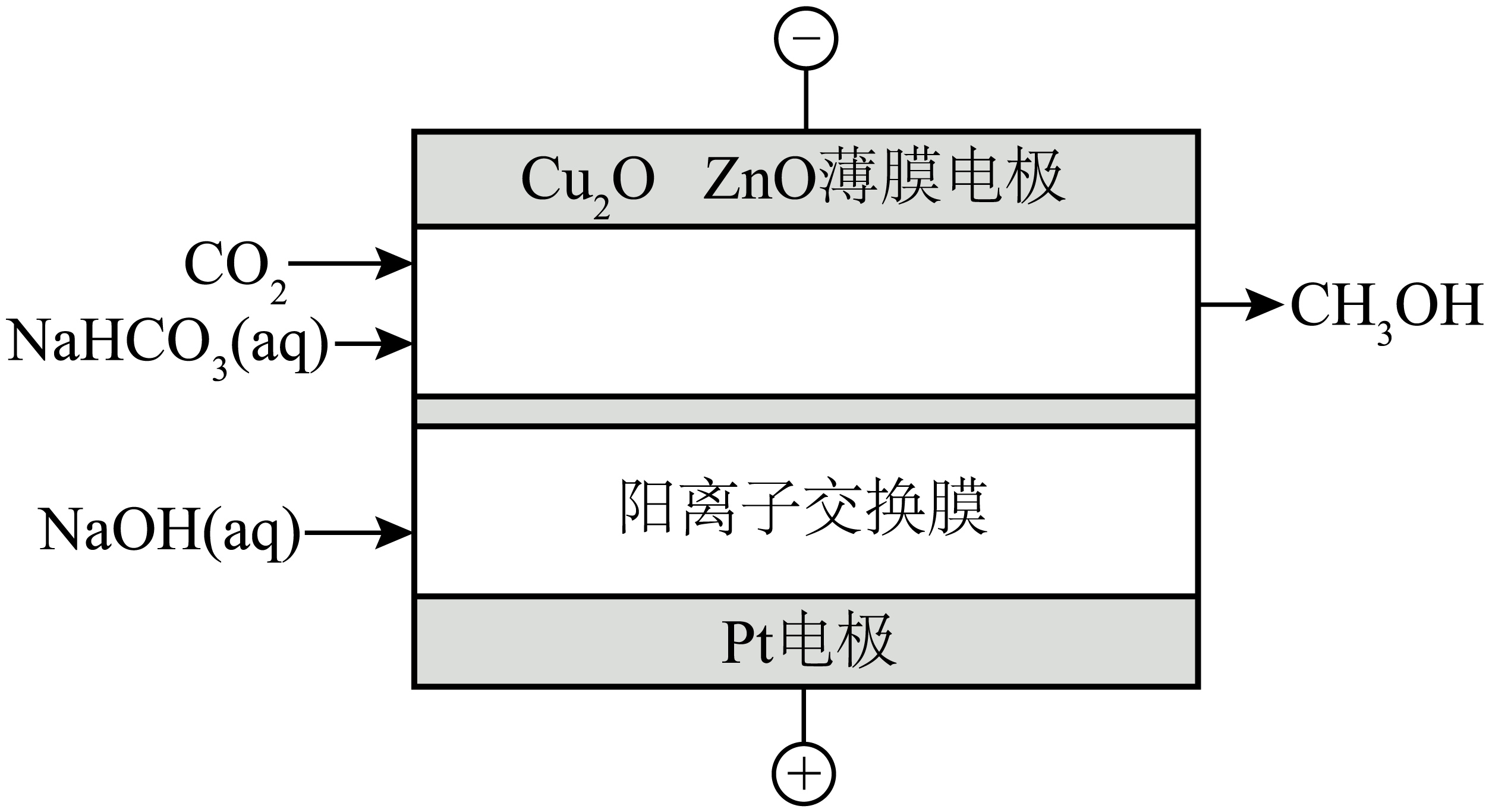
①阴极发生的反应方程式为                。

②当生成$16\ \text{g}$甲醇时，阳极区质量减少                $\operatorname{g}$。

$\\text{C}{{\\text{O}}_{2}}+6{{\\text{e}}^{-}}+6\\text{HCO}_{3}^{-}=\\text{C}{{\\text{H}}_{3}}\\text{OH}+{{\\text{H}}_{2}}\\text{O}+6\\text{CO}_{3}^{2-}$ ； $\\rm 93$

①二氧化碳在阴极发生还原反应，则电极反应为：$\text{C}{{\text{O}}_{2}}+6{{\text{e}}^{-}}+6\text{HCO}_{3}^{-}=\text{C}{{\text{H}}_{3}}\text{OH}+{{\text{H}}_{2}}\text{O}+6\text{CO}_{3}^{2-}$；

②阳极区反应为$\rm 4OH^{-}-4e^{-}=2H_{2}O+O_{2}↑$，同时会有$\rm 4$个钠离子向阴极移动，则当生成$16\ \text{g}$甲醇时，即$\rm 0.5\;\rm mol$甲醇生成时，会转移$\rm 3$ $\rm mol$电子，生成$\rm 0.75$ $\rm mol$氧气，同时会有$\rm 3$ $\rm mol$钠离子向阴极移动，质量减少$\rm 0.75$ $\rm mol\times 32$ $\rm g/mol+3$ $\rm mol\times 23$ $\rm g/mol=93$ $\rm g$。