一定压强下，由最稳定单质生成$\rm 1\;\rm mol$化合物的焓变为该物质的摩尔生成焓。已知$\text{CO}\left( \text{g} \right)$、${{\text{H}}_{2}}\text{O}\left( \text{g} \right)$的摩尔生成焓分别为$-110\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$、$-242\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$。则$\text{C}{{\text{O}}_{2}}$的摩尔生成焓的热化学方程式为                。

$\\text{C}\\left( \\text{s} \\right)+{{\\text{O}}_{2}}\\left( \\text{g} \\right)=\\text{C}{{\\text{O}}_{2}}\\left( \\text{g} \\right)\\text{ }\\!\\!\\qquad\\Delta{{\\textit{H}}_{4}}\\rm =-393\\;\\rm \\text{kJ}\\cdot \\text{mo}{{\\text{l}}^{-1}}$

已知：反应$\rm a$：$\text{CO}\left( \text{g} \right)+{{\text{H}}_{2}}\text{O}\left( \text{g} \right)=\text{C}{{\text{O}}_{2}}\left( \text{g} \right)+{{\text{H}}_{2}}\left( \text{g} \right)\text{ }\!\!\qquad\Delta{{\textit{H}}_{\text{1}}}=-41\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

一定压强下，由最稳定单质生成$\rm 1\;\rm mol$化合物的焓变为该物质的摩尔生成焓。已知$\text{CO}\left( \text{g} \right)$、${{\text{H}}_{2}}\text{O}\left( \text{g} \right)$的摩尔生成焓分别为$-110\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$、$-242\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$，则得：

$\rm b$．$\text{C}\left( \text{s} \right)+\dfrac{1}{2}{{\text{O}}_{2}}\left( \text{g} \right)=\text{CO}\left( \text{g} \right)\qquad\Delta{{\textit{H}}_{2}}=-110\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

$\rm c$．${{\text{H}}_{\text{2}}}\left( \text{g} \right)+\dfrac{1}{2}{{\text{O}}_{2}}\left( \text{g} \right)={{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right)\qquad\Delta{{\textit{H}}_{3}}=-242\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

$\rm d$．$\text{C}\left( \text{s}\right)+\text{O}_{2}\left( \text{g}\right)=\text{C}\text{O}_{2}\left( \text{g}\right)\qquad\Delta\textit{H}_{4}$

根据盖斯定律，由$\rm a+b+c$得反应$\rm d$．$\text{C}\left( \text{s} \right)+{{\text{O}}_{2}}\left( \text{g} \right)=\text{C}{{\text{O}}_{2}}\left( \text{g} \right)\qquad\Delta{{\textit{H}}_{4}}\rm =$ $\Delta{{\textit{H}}_{1}}\text{+ }\!\!\Delta{{\textit{H}}_{2}}\text{+ }\!\!\Delta{{\textit{H}}_{3}}\rm =$ $-41\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}-110\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}-242\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}\rm =$ $-393\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$，因此$\text{C}{{\text{O}}_{2}}$的摩尔生成焓的热化学方程式为$\text{C}\left( \text{s} \right)+{{\text{O}}_{2}}\left( \text{g} \right)=\text{C}{{\text{O}}_{2}}\left( \text{g} \right)\qquad\Delta{{\textit{H}}_{4}}\rm =-393\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$；

实验发现，其他条件不变，在相同时间内，向上述体系中投入一定量的$\rm CaO$可以增大$\rm H$₂的体积分数。对比实验的结果如下图所示。投入$\rm CaO$时，${{\text{H}}_{2}}$的体积分数增大的原因为                。投入纳米$\rm CaO$装置的氢气产率更高，其原因为                。

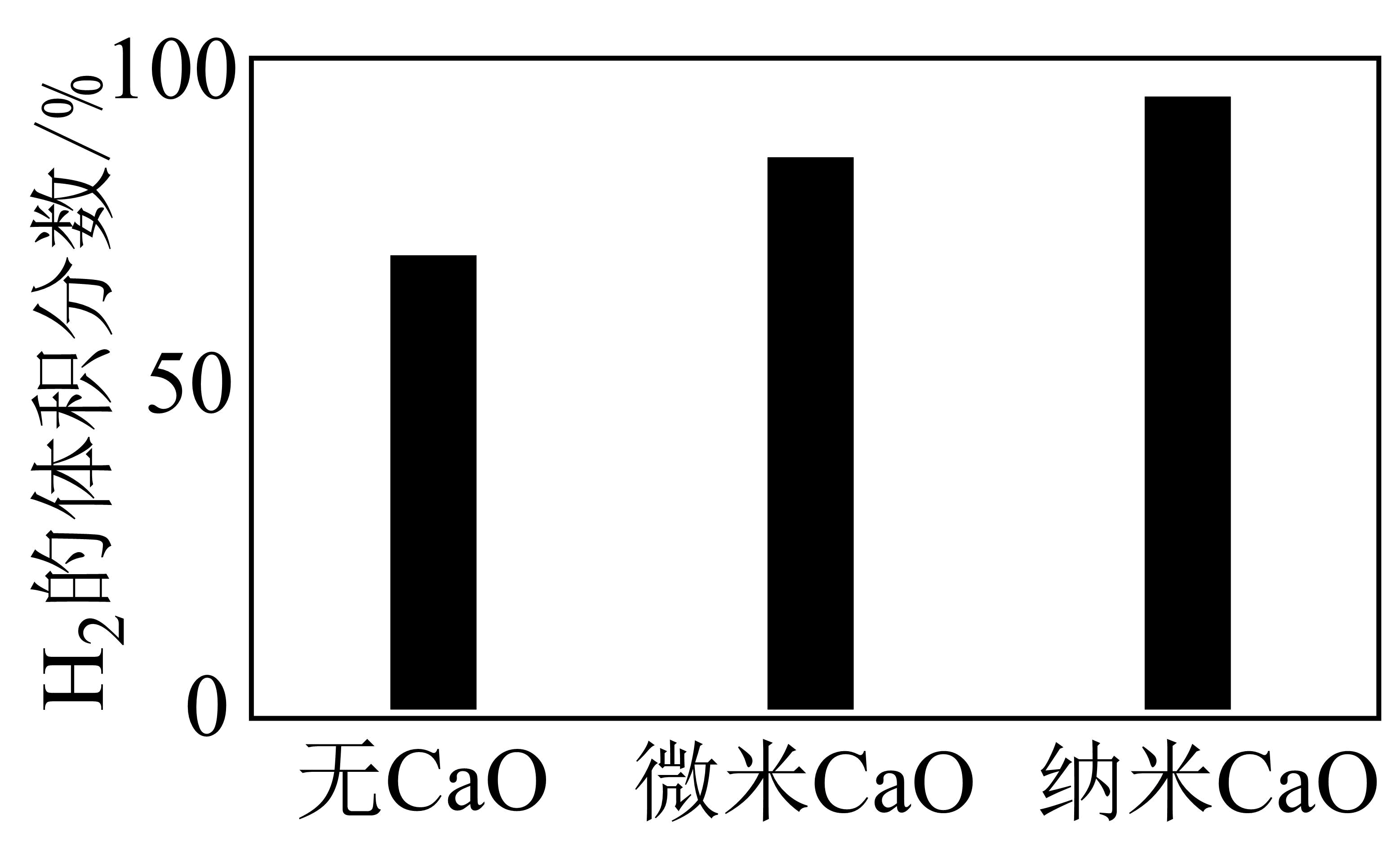
$\\rm CaO$可以吸收$\\rm CO_{2}$，使$\\rm CO_{2}$浓度减小，生成$\\rm H_{2}$的反应正向移动，$\\rm H_{2}$百分含量增大；纳米$\\rm CaO$表面积比微米$\\rm CaO$大，吸收$\\rm CO_{2}$能力比微米$\\rm CaO$强

催化重整后的化学方程式为$\rm CH_{4}(g)+2H_{2}O(g)⇌CO_{2}(g)+4H_{2}(g)$，向其中投入$\rm CaO$时，$\rm CaO$可吸收$\rm CO_{2}$，使$c$($\rm CO_{2}$)减小，平衡正向移动，导致生成$\rm H_{2}$更多，$\rm H_{2}$百分含量增大，若投入纳米$\rm CaO$时，由于纳米$\rm CaO$颗粒小，表面积大，可使反应速率加快，$c$($\rm CO_{2}$)减小，平衡正向移动加剧，所以$\rm H_{2}$百分含量增大

酸性溶液中电解副产物$\text{C}{{\text{O}}_{2}}$可用于生产$\text{C}{{\text{H}}_{3}}\text{OH}$，实现$\text{C}{{\text{O}}_{2}}$的资源化，其电极反应式为                。生成$\text{C}{{\text{H}}_{3}}\text{OH}$的电极应连接电源的                极$\rm ($选填“正”或“负”$\rm )$。

$\\rm CO_{2}+6H^{+}+6e^{-}=CH_{3}OH+H_{2}O$ ；负

$\rm CO_{2}$也可在酸性水溶液中通过电解生成甲醇，$\rm C$元素化合价降低，被还原，应为电解池的阴极反应，连接电源的负极；电极方程式为$\rm CO_{2}+6H^{+}+6e^{-}=CH_{3}OH+H_{2}O$

Ⅱ.甲烷干重整(DRM)

DRM的主要反应为：

反应b：$\text{C}{{\text{H}}_{4}}\left( \text{g} \right)+\text{C}{{\text{O}}_{2}}\left( \text{g} \right)\rightleftharpoons 2\text{CO}\left( \text{g} \right)+2{{\text{H}}_{2}}\left( \text{g} \right)\qquad\Delta{{\textit{H}}_{2}}=+249.1\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

反应c：${{\text{H}}_{2}}\left( \text{g} \right)+\text{C}{{\text{O}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{CO}\left( \text{g} \right)+{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\qquad\Delta{{\textit{H}}_{3}}=+41\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

该过程中会逐渐生成积碳覆盖在催化剂$\rm CeO_2$表面，使催化剂中毒。

甲烷和二氧化碳的起始物质的量均为$\rm 1\;\rm mol$，实验测得在$\rm 0.1\ MPa$下，平衡时各组分的量随温度变化如下图所示。已知气体分压$\rm =$气体总压$\rm \times $气体的物质的量分数，用平衡分压代替平衡浓度可以得到平衡常数$\textit{K}_{\text{p}}$。$\rm 625^\circ C$时反应$\rm c$的压强平衡常数$\textit{K}_{\text{p}}$为                。

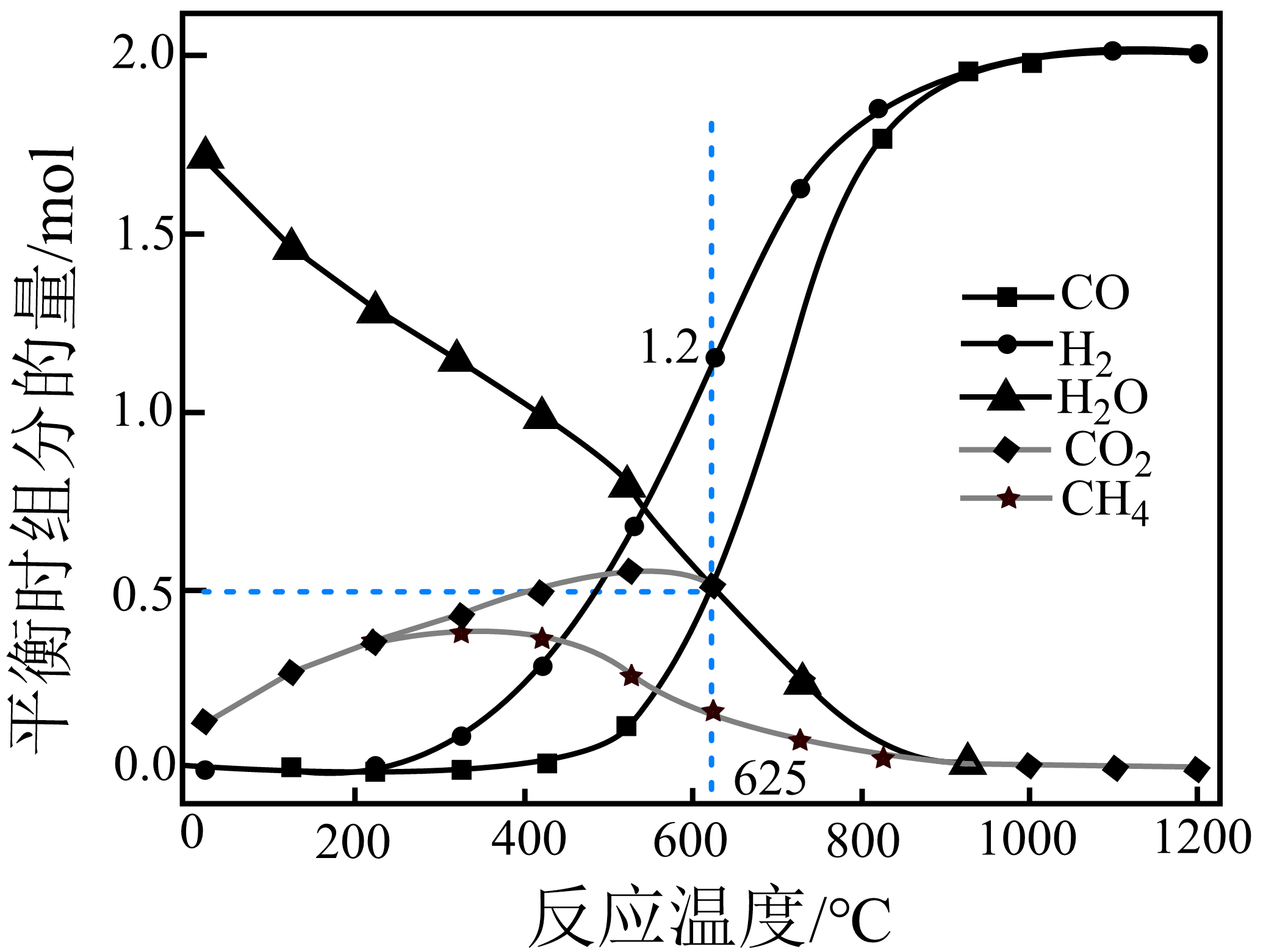
$\\dfrac{5}{12}$

由图知，$\rm 625\;\rm ^\circ\rm C$达到平衡时，$n\rm(H_{2}O)=\textit{n}\rm(CO_{2})=\textit{n}(CO)=0.5\;\rm mol$，氢气是$\rm 1.2\;\rm mol$，根据氢原子守恒，平衡时甲烷物质的量为$\dfrac{4-2.4-1}{4}\rm mol=0.15$ $\rm mol$，根据碳原子守恒知，积碳的物质的量为（$\rm 1+1-0.5-0.5-0.15$）$\rm mol=0.85\;\rm mol$；反应Ⅱ的压强平衡常数$K_\rm p=\dfrac{\textit{p}(\text{CO})\textit{p}(\text{H}_{\text{2}}\text{O})}{\textit{p}(\text{H}_{\text{2}})\textit{p}(\text{C}\text{O}_{\text{2}})}=\dfrac{\textit{n}(\text{CO})\textit{n}(\text{H}_{\text{2}}\text{O})}{\textit{n}(\text{H}_{\text{2}})\textit{n}(\text{C}\text{O}_{\text{2}})}=\dfrac{0.5\times0.5}{1.2\times0.5}=\dfrac{5}{12}$；

对催化剂载体$\mathrm{CeO}_{2}$改性，使其形成氧空位，可减少积碳。$\mathrm{CeO}_{2}$晶胞如下图所示。取干燥$\mathrm{CeO}_{2}$在$\rm Ar$气条件下加热，热重分析显示样品一直处于质量损失状态；$\rm X$射线衍射分析结果表明随着温度升高，该晶胞边长变长，但铈离子空间排列没有发生变化。加热后，当失重率$\rm ($损失的质量$\rm /$总质量$\rm )$为$\rm 2.32\%$时，每个晶胞拥有的${{\text{O}}^{{{2-}}}}$的个数为                。

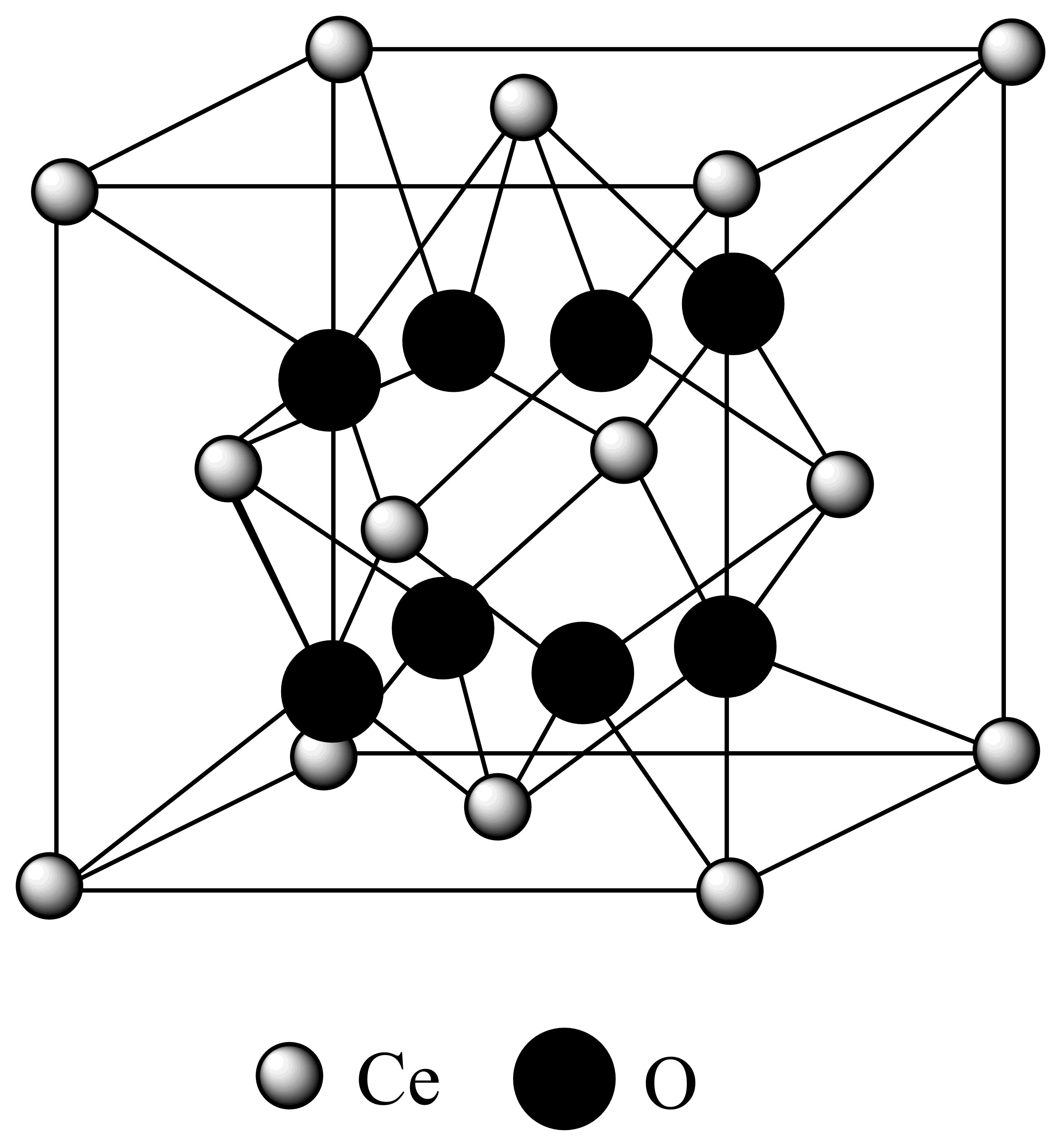
$\\rm 7$

一个$\mathrm{CeO}_{2}$晶胞中$\rm Ce^{4+}$个数为$8\times \dfrac{1}{8}+6\times \dfrac{1}{2}=4$、$\rm O^{2-}$在体内，个数为$\rm 8$，即一个$\mathrm{CeO}_{2}$晶胞中$\rm 4$个$\rm Ce^{4+}$、$\rm 8$个$\rm O^{2-}$，$\rm 1\;\rm mol\;\rm CeO_{2}$质量为$\rm 172\;\rm g$，加热后当失重率为$\rm 2.32\%$时，损失的质量为氧元素的质量，即$\rm 172\;\rm g\times 2.32\%=4.0\;\rm g$，$n\rm (O)=0.25\;\rm mol$，因为铈离子空间排列没有发生变化，所以失去$\rm O^{2-}$的个数为$\rm 0.25\times 4=1$，每个晶胞拥有的$\rm O^{2-}$的个数为$\rm 8-1=7$。