一种钽$\rm (Ta)$的化合物的四方晶胞结构如图所示$(b\lt 2a\rm )$。已知${{N}_{\rm A}}$为阿伏加德罗常数的值。原子分数坐标$x$、$y$、$z\in [0,1)$，原子分数坐标为$\rm 1$时记为$\rm 0$。$\rm M$、$\rm N$的原子分数坐标分别为$\rm (0,0,0)$，$\rm (0,0,1/2)$，下列说法错误的是$\rm (\qquad)$

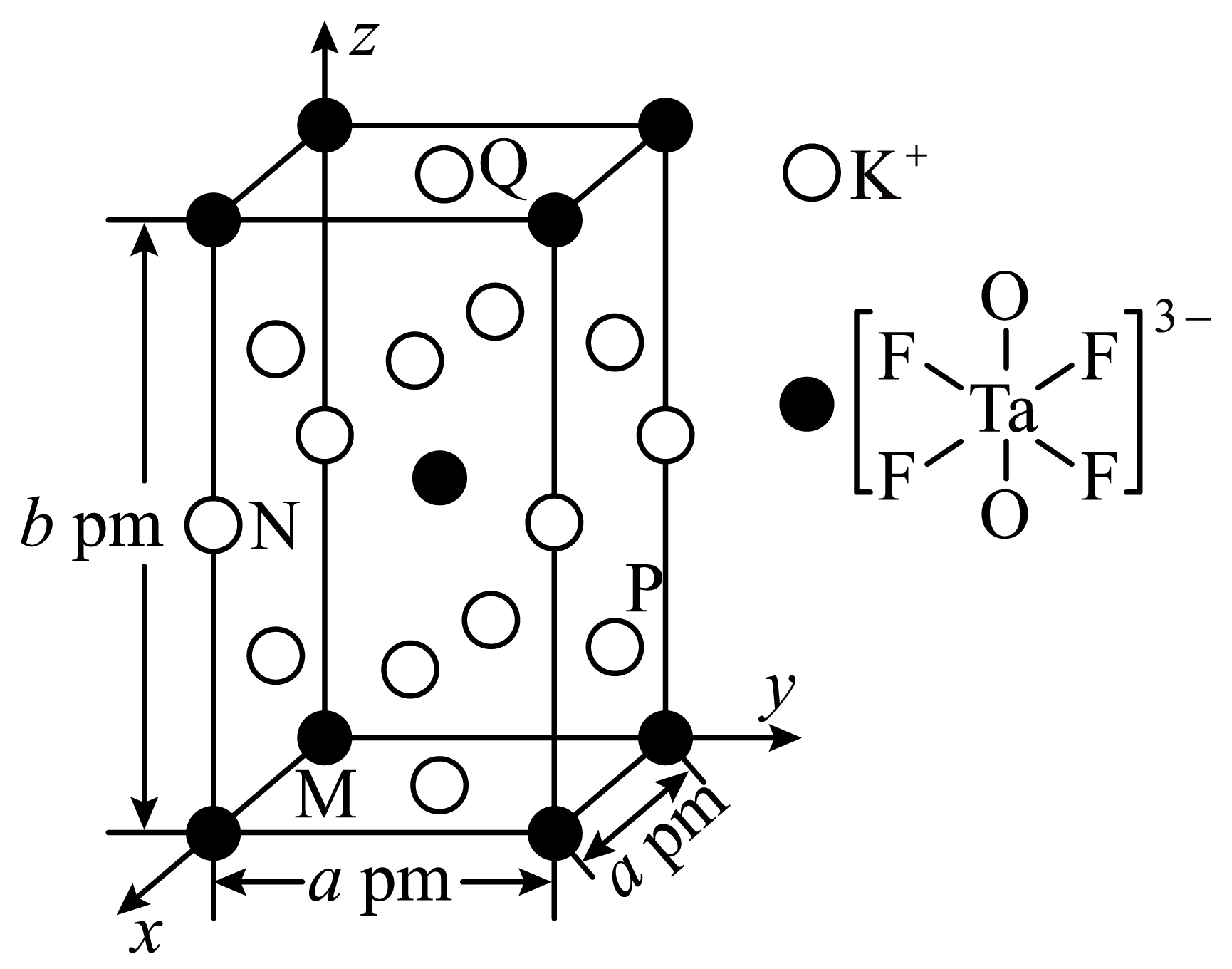
$\\rm P$的原子分数坐标为$\\rm (1/2,0,1/4)$

该化合物的化学式为$\\rm {{K}_{3}}Ta{{O}_{2}}{{F}_{4}}$

与$\\rm Q$距离相等且最近的$\\rm {{K}^{+}}$有$\\rm 8$个

该晶体的密度是$\\dfrac{4.06\\times {{10}^{32}}}{{{a}^{2}}b{{N}_{\\rm A}}}\\ \\rm g/c{{m}^{3}}$

$\rm A$．已知原子分数坐标为$\rm 1$时记为$\rm 0$，$\rm P$在$x$轴的坐标分数为$\rm \dfrac{1}{2}$，在$y$轴的坐标分数为$\rm 1$，则记为$\rm 0$，$z$轴坐标分数为$\rm \dfrac{1}{4}$，故$\rm P$的原子分数坐标为$\rm (\dfrac{1}{2},0,\dfrac{1}{4})$，$\rm A$正确；

$\rm B$．根据均摊法，$\rm {{K}^{+}}$的个数是$\rm 4\times \dfrac{1}{4}+10\times \dfrac{1}{2}=6$，$\rm {{(Ta{{O}_{2}}{{F}_{4}})}^{3-}}$的个数是$\rm 8\times \dfrac{1}{8}+1=2$，则晶胞的化学式为$\rm {{K}_{3}}Ta{{O}_{2}}{{F}_{4}}$，$\rm B$正确；

$\rm C$．与$\rm Q$距离相等且最近的$\rm {{K}^{+}}$分别位于上下两个晶胞的面上，因此，与$\rm Q$距离相等且最近的$\rm {{K}^{+}}$共有$\rm 8$个，$\rm C$正确；

$\rm D$．由$\rm B$选项可知，一个晶胞含有两个$\rm {{K}_{3}}Ta{{O}_{2}}{{F}_{4}}$，则晶胞的质量为$\dfrac{2\times (39\times 3+181+16\times 2+19\times 4)}{{{N}_{\rm A}}}\ {\rm g}=\dfrac{812}{{{N}_{\rm A}}}\ \rm g$，晶胞的体积为${{a}^{2}}b\times {{10}^{-30}}\rm \ c{{m}^{3}}$，则该晶体的密度是$\dfrac{8.12\times {{10}^{32}}}{{{a}^{2}}b{{N}_{\rm A}}}\ \rm g/c{{m}^{3}}$，$\rm D$错误；

故选：$\rm D$