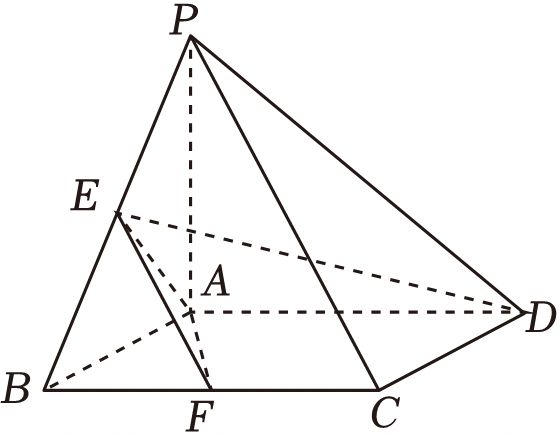
如图，在四棱锥$P-ABCD$中，底面$ABCD$为矩形，$PA\perp$平面$ABCD$，$E$，$F$分别为$PB$，$BC$的中点，则$AF\perp DE$的一个充要条件为$(\qquad)$．

$PA=AB$

$PF\\perp BD$

$AB=AD$

$AB=\\sqrt{2}AD$

$\because PA\perp$平面$ABCD$且底面$ABCD$为矩形，故可建立如图所示的空间直角坐标系，

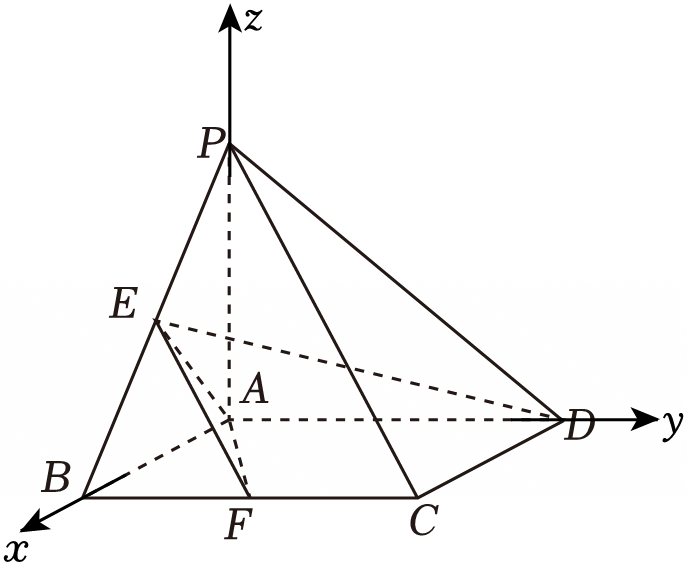
则$A(0,0,0)$，设$\vert AB\vert =2a$，$\vert AD\vert =2b$，$\vert PA\vert =m$，

则$B(2a,0,0)$，$P(0,0,m)$，$D(0,2b,0)$，

$\because E$，$F$分别为$PB$，$BC$的中点，

则$E\left(a,0,\dfrac{m}{2}\right)$，$F(2a,b,0)$，

故$\overrightarrow{AF}=(2a,b,0)$，$\overrightarrow{DE}=\left(a,-2b,\dfrac{m}{2}\right)$，

$\because AF\perp DE$的充要条件为$\overrightarrow{AF}\cdot \overrightarrow{DE}=0$，即$2a^{2}-2b^{2}-0\cdot \dfrac{m}{2}=0$

解得$a=b$，即$AF\perp DE$的充要条件为$a=b$，故$\rm C$正确，$\rm D$错误；

$PA=AB$即$2a=m$，此时得不到$2a=2b$，故$\rm A$错误；

对于$\rm B$，$\overrightarrow{PF}=(2a,b,-m)$，$\overrightarrow{BD}=(-2a,2b,0)$，

若$PF\perp BD$，则$\overrightarrow{PF}\cdot \overrightarrow{BD}=0$，即$-4a^{2}+2b^{2}-m\cdot 0=0$，解得$\sqrt{2}a=b$，

由$A$的分析可得$AF\perp DE$的充要条件为不是$PF\perp BD$，故$\rm B$错误．

故选：$\rm C$