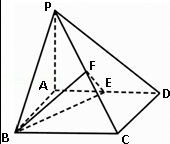
如图，四边形$ABCD$是矩形，$PA\perp$平面$ABCD$，$AP=AB=2$，$BC=2\sqrt{2}$，$E$，$F$分别是$AD$，$PC$的中点．建立适当的空间坐标系，利用空间向量详解以下问题：

$(1)$证明：$PC\perp$平面$BEF$；

$(2)$求平面$BEF$与平面$BAP$夹角的大小．

$(1)$证明见解析；

$(2)$$45^\\circ$

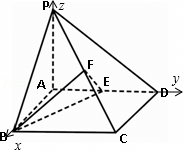
$(1)$证明：如图，以$A$为坐标原点，$AB$，$AD$，$AP$所在直线分别为$x$，$y$，$z$轴建立空间直角坐标系．

$\because AP=AB=2,BC=AD=2\sqrt{2}$，四边形$ABCD$是矩形．

$\therefore A$，$B$，$C$，$D$，$P$的坐标为$A(0$，$0$，$0)$，$B(2$，$0$，$0)$，$C(2,2\sqrt{2},0)D(0,2\sqrt{2},0),P(0,0,2)$，

又$E$，$F$分别是$AD$，$PC$的中点，

$\therefore E(0,\sqrt{2},0),F(1,\sqrt{2},1)$，

$\therefore \overrightarrow{PC}=(2,2\sqrt{2},-2),\overrightarrow{BF}=(-1,\sqrt{2},1),\overrightarrow{EF}=(1,0,1)$，

$\therefore \overrightarrow{PC}\cdot \overrightarrow{BF}=-2+4-2=0,\overrightarrow{PC}\cdot \overrightarrow{EF}=2+0-2=0$，

$\therefore \overrightarrow{PC}\perp \overrightarrow{BF},\overrightarrow{PC}\perp \overrightarrow{EF}$，

又$\because BF\cap EF=F$，

$\therefore PC\perp$平面$BEF$

$(2)$解：由$(1)$知平面$BEF$的法向量$\overrightarrow{n_1}=\overrightarrow{PC}=(2,2\sqrt{2},-2)$，

平面$BAP$的法向量$\overrightarrow{n_2}=\overrightarrow{AD}=(0,2\sqrt{2},0)$，

$\therefore \overrightarrow{n_1}\cdot \overrightarrow{n_2}=8$

设平面$BEF$与平面$BAP$的夹角为$\theta$，

则$\cos \theta =\cos \lt \overrightarrow{n_1},\overrightarrow{n_2}\gt =\dfrac{\overrightarrow{n_1}\cdot \overrightarrow{n_2}}{\vert \overrightarrow{n_1}\vert \vert \overrightarrow{n_2}\vert }=\dfrac{8}{4\times 2\sqrt{2}}=\dfrac{\sqrt{2}}{2}$，

$\therefore \theta =45^\circ$，

$\therefore $平面$BEF$与平面$BAP$的夹角为$45^\circ$