| 7.3.2 正弦型函数的性质与图像 题目答案及解析
稿件来源:高途
| 7.3.2 正弦型函数的性质与图像题目答案及解析如下,仅供参考!
必修三
第七章 三角函数
7.3 三角函数的性质与图像
7.3.2 正弦型函数的性质与图像
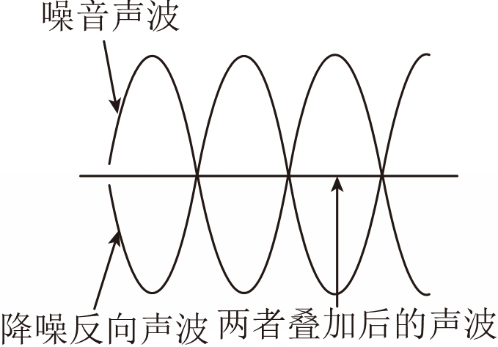
科技的发展改变了世界,造福了人类,我们生活中处处享受着科技带来的“红利”.例如主动降噪耳机让我们在嘈杂的环境中享受一丝宁静,它的工作原理是:先通过微型麦克风采集周围的噪声,然后降噪芯片生成与噪声振幅相同、相位相反的声波来抵消噪声(如图所示).已知某噪声声波曲线为$f(x)=2\sin \left(\dfrac{2\pi }{3}x+\varphi \right)\left(\vert \varphi \vert \lt \dfrac{\pi }{2}\right)$,且经过点$(1,2)$,降噪芯片生成的降噪反向声波曲线为$g(x)$.下述四个结论:
①函数$g\left(x+\dfrac{1}{4}\right)$是奇函数;
②函数$g(x)$在区间$(1,2)$上单调递减;
③对于$\forall x\in {\bf R}$,都有$f(x+1)+f(x+2)+f(x+3)=0$;
④$\exists n\in {\bf N}^{*}$,使得$f(1)+f(2)+f(3)+\cdots \cdots +f(n)\gt 2$.
其中所有正确结论的编号是 .
$\because f(x)=2\sin \left(\dfrac{2\pi }{3}x+\varphi \right)$经过$(1,2)$,
$\therefore \sin \left(\dfrac{2\pi }{3}+\varphi \right)=1$,即$\dfrac{2\pi }{3}+\varphi =\dfrac{\pi }{2}+2k\pi$,
解得$\varphi =-\dfrac{\pi }{6}+2k\pi$,$k\in {\bf Z}$;
$\because \vert \varphi \vert \lt \dfrac{\pi }{2}$,
$\therefore \varphi =-\dfrac{\pi }{6}$,$f(x)=2\sin \left(\dfrac{2\pi }{3}x-\dfrac{\pi }{6}\right)$.
对于①,令$f(x)$的周期为$T$,则$T=\dfrac{2\pi }{\dfrac{2\pi }{3}}=3$,
由图可知,将噪声声波曲线向左平移$\dfrac{T}{2}=\dfrac{3}{2}$,即可得到降噪反向声波曲线,
$g(x)=f\left(x+\dfrac{3}{2}\right)=2\sin \left[\dfrac{2\pi }{3}\left(x+\dfrac{3}{2}\right)-\dfrac{\pi }{6}\right]=2\sin \left(\dfrac{2\pi }{3}x+\dfrac{5\pi }{6}\right)$,
$g\left(x+\dfrac{1}{4}\right)=2\sin \left[\dfrac{2\pi }{3}\left(x+\dfrac{1}{4}\right)+\dfrac{5\pi }{6}\right]=-2\sin \dfrac{2\pi }{3}x$,
$\therefore g\left(x+\dfrac{1}{4}\right)$为奇函数,故①正确;
对于②,$x\in (1,2)$时,$\dfrac{2\pi }{3}x-\dfrac{\pi }{6}\in \left(\dfrac{\pi }{2},\dfrac{7\pi }{6}\right)$,
结合正弦函数的图象知$x\in (1,2)$时,$f(x)$单调递减,
$\therefore g(x)$单调递增,故②错误;
对于④,$f(x+1)+f(x+2)+f(x+3)$,
$\therefore f(x+1)+f(x+2)+f(x+3)$恒为$0$,故④正确;
对于③,当$n=3k$,$k\in {\bf N}^{*}$时,$f$$(1)$$+f$$(2)$$+f$$(3)$$+\dotsb +f(n)=0$,
当$n=3k+1$,$k\in {\bf N}^{*}$时,
当$n=3k+2$,$k\in {\bf N}^{*}$时,取等号,故③错误.
故答案为:①④
| 7.3.2 正弦型函数的性质与图像题目答案及解析(完整版)
