如图，直线$AB$与半径为$1$的圆$C$相切于$D$点，射线$DB$绕着$D$点逆时针方向旋转到$DA$，在旋转过程中射线$DB$交圆$C$于$E$点，设$\angle BDE=x$，$x\in \left[0,\pi \right]$，且恒满足$\angle DCE=2\angle BDE$，射线$DB$扫过圆$C$内部（阴影部分）的面积为$S=f\left(x\right)$，则下列正确的是$ $ $(\qquad)$ $ $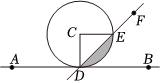

$f(\\dfrac{\\pi }{4})=\\dfrac{\\pi }{4}-\\dfrac{1}{2}$

$f\\left(x\\right)$的单调递增区间为$(0,\\dfrac{\\pi }{2})$

点$(\\dfrac{\\pi }{2},\\dfrac{\\pi }{2})$为$f\\left(x\\right)$的对称中心

$f\\left(x\\right)$在$x=\\dfrac{\\pi }{2}$瞬时变化率最大

$\rm A:\because S=f(x)=\dfrac{1}{2}×{1}^{2}×2x-\dfrac{1}{2}×{1}^{2}×\sin2x=x-\dfrac{1}{2}\sin2x,x∈[0,\pi ],f(\dfrac{\pi }{4})=\dfrac{\pi }{4}-\dfrac{1}{2}$，所以本选项正确；
$\rm B$：因为${f}'\left(x\right)=1-\cos 2x\geqslant 0$，故$f\left(x\right)$的单增区间为$\left[0,\pi \right]$，因此本选项错误；
$\rm C$：因为$f(x)+f(\pi -x)=x-\dfrac{1}{2}\sin2x+\pi -x-\dfrac{1}{2}\sin(2\pi -2x)=\pi $，
所以点$(\dfrac{\pi }{2},\dfrac{\pi }{2})$为$f\left(x\right)$的对称中心，因此本选项正确；
$\rm D$：因为$f′(\dfrac{\pi }{2})=2≥f′(x)$，故$f\left(x\right)$在$x=\dfrac{\pi }{2}$瞬时变化率最大，因此本选项正确.
故选：$\rm ACD $.