已知函数$f(x)=2\sin({\omega x+\phi })({\omega \gt 0,|\phi |\lt \dfrac{\pi }{2}})$的部分图象如图所示，则满足条件$({f(x)+f({-\dfrac{{5\pi }}{4}})})({f(x)+f({\dfrac{{7\pi }}{3}})})\lt 0$的最小正偶数$x$为                  .

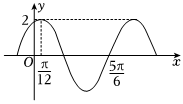
由图可知$\dfrac{3}{4}T=\dfrac{5\pi }{6}-\dfrac{\pi }{12}=\dfrac{3\pi }{4}$，即$T=\dfrac{2\pi }{\omega }=\pi $，所以$\omega =2$，
由五点法可得$2\times \dfrac{\pi }{12}+\varphi =\dfrac{\pi }{2}$，即$\varphi =\dfrac{\pi }{3}$，
所以，$f\left(x\right)=2\sin (2x+\dfrac{\pi }{3})$，
因为$f(-\dfrac{5\pi }{4})=2\sin (-\dfrac{5\pi }{2}+\dfrac{\pi }{3})=-1$，$f(\dfrac{7\pi }{3})=2\sin (\dfrac{14\pi }{3}+\dfrac{\pi }{3})=0$，
所以由$({f(x)+f({-\dfrac{{5\pi }}{4}})})({f(x)+f({\dfrac{{7\pi }}{3}})})\lt 0$，可得$\left(f\left(x\right)-1\right)f\left(x\right) \lt 0$，
解得$0 \lt f\left(x\right) \lt 1$，即$\sin (2x+\dfrac{\pi }{3})\in (0$，$\dfrac{1}{2})$，
所以$2k\pi\ \ \lt 2x+\dfrac{\pi }{3} \lt 2k\pi +\dfrac{\pi }{6}$，$k\in \bf Z$，或$2k\pi +\dfrac{5\pi }{6} \lt 2x+\dfrac{\pi }{3} \lt 2k\pi +\pi $，$k\in \bf Z$，
解得$k\pi -\dfrac{\pi }{6} \lt x \lt k\pi -\dfrac{\pi }{12}$，$k\in \bf Z$，或$k\pi +\dfrac{\pi }{4} \lt x \lt k\pi +\dfrac{\pi }{3}$，$k\in \bf Z$，
令$k=1$，可得$\dfrac{5\pi }{6} \lt x \lt \dfrac{11\pi }{12}$，或$\dfrac{5\pi }{4} \lt x \lt \dfrac{4\pi }{3}$，
所以最小正偶数$x$为$4$.
故答案为：$4$.