以下四个命题表述正确的是$(\qquad)$．

若直线$l$的斜率为$-\\sqrt{3}$，则直线$l$的倾斜角为$-\\dfrac{\\pi }{3}$

三棱锥$P-ABC$中，$E$，$F$分别为$PB$，$PC$的中点，$\\overrightarrow{PG}=\\dfrac{2}{3}\\overrightarrow{PA}$，则平面$EFG$将该三棱锥所分的两部分几何体的体积之比为$1:5$，即$V_{P-EFG}:V_{EFG-ABC}=1:5$

若直线$l$过点$P(2,-1)$且在两坐标轴上的截距之和为$0$，则直线$l$的方程为$x-y-3=0$

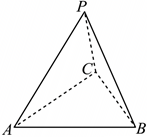
在四面体$O-ABC$中，若$OA\\perp BC$，$OB\\perp AC$，则$OC\\perp AB$

对于$\rm A$，若直线$l$的斜率为$-\sqrt{3}$，则直线$l$的倾斜角为$\dfrac{2\pi }{3}$，故$\rm A$错误；

对于$\rm B$，设点$A$到平面$PBC$的距离为$h$，点$G$到平面$PBC$的距离为$h'$，

$\because \overrightarrow{PG}=\dfrac{2}{3}\overrightarrow{PA}$，

$\therefore h'=\dfrac{2}{3}h$，

$\because E$，$F$分别为$PB$，$PC$的中点，

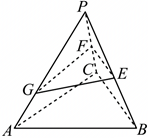
$\therefore {S_{\triangle PEF}}=\dfrac{1}{4}{S_{\triangle PBC}}$，

则${V_{P-ABC}}={V_{A-PBC}}=\dfrac{1}{3}{S_{\triangle PBC}}h$，${V_{P-GEF}}={V_{G-PEF}}=\dfrac{1}{3}\cdot \dfrac{1}{4}{S_{\triangle PBC}}\cdot \dfrac{2}{3}h=\dfrac{1}{6}{V_{P-ABC}}$，

则${V_{EFG-ABC}}={V_{P-ABC}}-{V_{P-EFG}}=\dfrac{5}{6}{V_{P-ABC}}$，

$\therefore V_{P-EFG}:V_{EFG-ABC}=1:5$，故$\rm B$正确；

对于$\rm C$，当直线$l$不过原点时，设直线方程为$\dfrac{x}{a}+\dfrac{y}{-a}=1$，

则有$\dfrac{2}{a}+\dfrac{-1}{-a}=1$，解得$a=3$，

$\therefore $ 直线方程为$\dfrac{x}{3}-\dfrac{y}{3}=1$，即$x-y-3=0$，

当直线$l$过原点时，直线方程为$y=-\dfrac{1}{2}x$，

综上，所求直线方程为$y=-\dfrac{1}{2}x$或$x-y-3=0$；故$\rm C$错误．

对于$\rm D$，在四面体$O-ABC$中，$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$，$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}$，$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}$，

$\because OA\perp BC$，$OB\perp AC$，

$\therefore \overrightarrow{OA}\cdot \overrightarrow{BC}=\overrightarrow{OA}\cdot (\overrightarrow{OC}-\overrightarrow{OB})=0,\overrightarrow{OB}\cdot \overrightarrow{AC}=\overrightarrow{OB}\cdot (\overrightarrow{OC}-\overrightarrow{OA})=0$，

即$\overrightarrow{OA}\cdot \overrightarrow{OC}=\overrightarrow{OA}\cdot \overrightarrow{OB},\overrightarrow{OB}\cdot \overrightarrow{OC}=\overrightarrow{OA}\cdot \overrightarrow{OB}$，

$\therefore \overrightarrow{OA}\cdot \overrightarrow{OC}=\overrightarrow{OB}\cdot \overrightarrow{OC}$，

即$(\overrightarrow{OA}-\overrightarrow{OB})\cdot \overrightarrow{OC}=0$，

$\therefore \overrightarrow{BA}\cdot \overrightarrow{OC}=0$，

$\therefore AB\perp OC$，故$\rm D$正确．

故选：$\rm BD$