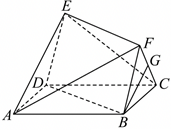
如图，已知多面体$ABCDEF$的底面$ABCD$为矩形，四边形$BDEF$为平行四边形，平面$FBC\perp$平面$ABCD$，$FB=FC=BC=1$，$AB=2$，$G$是$CF$的中点．

$(1)$证明：$BG//$平面$AEF$；

$(2)$在棱$CF$（不包括端点）上是否存在点$P$，使得平面$BDP$与平面$BCF$的夹角为$60^\circ$？若存在，求$CP$的长度；若不存在，请说明理由．

$(1)$证明见解析；

$(2)$不存在，理由见解析．

$(1)$证明：如图，取$BC$中点$N$，取$AD$中点$M$，连接$FN$，$MN$，

$\because \triangle FBC$为等边三角形，

$\therefore FN\perp BC$，

$\because $ 平面$FBC\perp$平面$ABCD$，

又$FN\subset$平面$FBC$，平面$FBC\cap$平面$ABCD=BC$，

$\therefore FN\perp$平面$ABCD$，

又底面$ABCD$为矩形，则$NM\perp NB$，

以$N$为坐标原点，$\overrightarrow{NM}$，$\overrightarrow{NB}$，$\overrightarrow{NF}$方向分别为$x$轴，$y$轴，$z$轴的正方向，建立空间直角坐标系$N-xyz$，

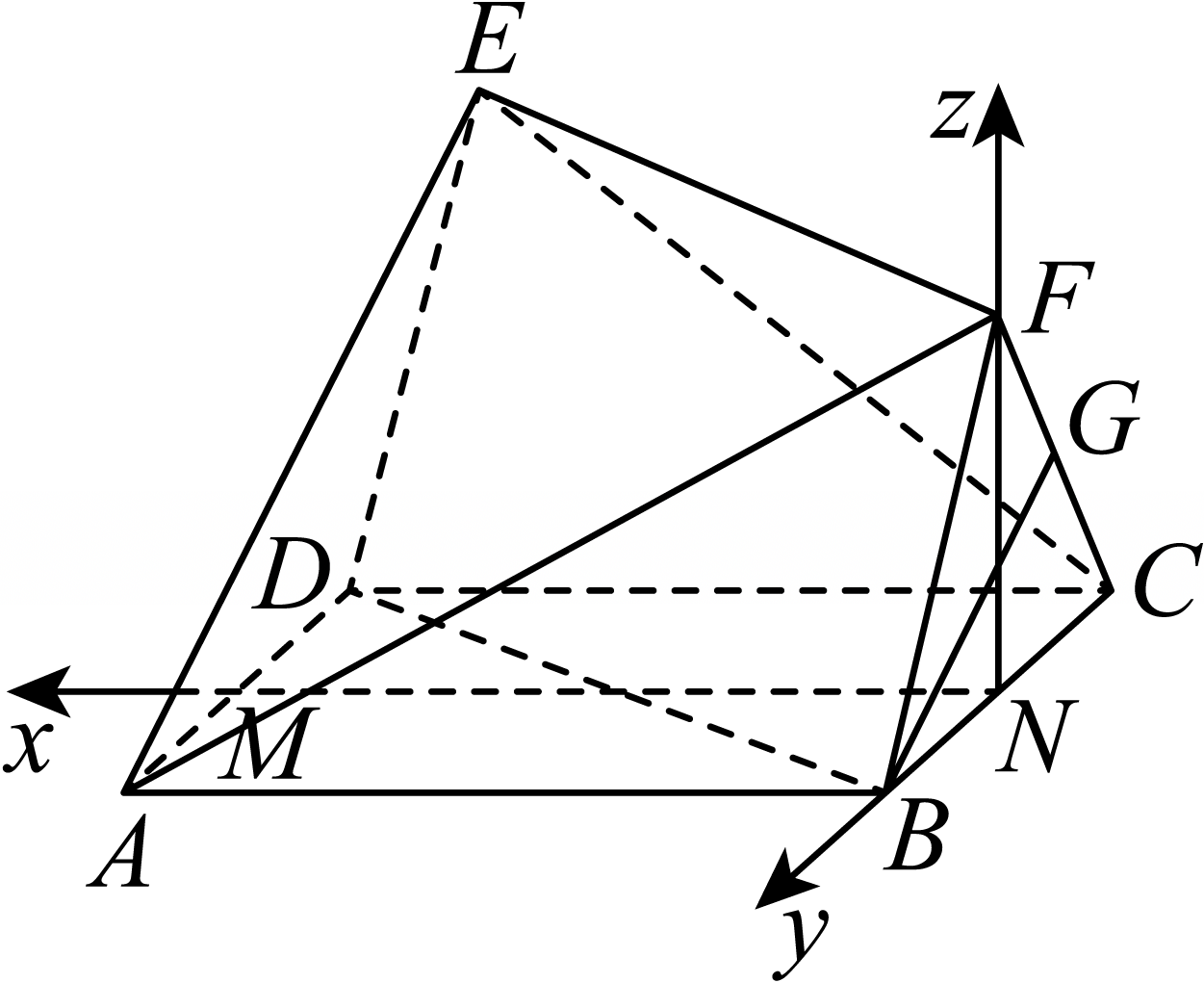
由题意可得，$A\left(2,\dfrac{1}{2},0\right)$，$B\left(0,\dfrac{1}{2},0\right)$，$C\left(0,-\dfrac{1}{2},0\right)$，$D\left(2,-\dfrac{1}{2},0\right)$，$F\left(0,0,\dfrac{\sqrt{3}}{2}\right)$，

已知$G$是$CF$的中点．则$G\left(0,-\dfrac{1}{4},\dfrac{\sqrt{3}}{4}\right)$，

可知$\overrightarrow{BG}=\left(0,-\dfrac{3}{4},\dfrac{\sqrt{3}}{4}\right)$，$\overrightarrow{AF}=\left(-2,-\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)$，$\overrightarrow{BD}=(2,-1,0)$，

由四边形$BDEF$为平行四边形，

得$\overrightarrow{AE}=\overrightarrow{AF}+\overrightarrow{BD}=\left(0,-\dfrac{3}{2},\dfrac{\sqrt{3}}{2}\right)$，

设平面$AEF$的法向量$\boldsymbol {n}=(x,y,z)$，

则$\begin{cases}{\boldsymbol {n}\cdot \overrightarrow{AF}=0}\\ {\boldsymbol {n}\cdot \overrightarrow{AE}=0}\end{cases}$，则$\begin{cases}-2x-\dfrac{1}{2}y+\dfrac{\sqrt{3}}{2}z=0\\ -\dfrac{3}{2}y+\dfrac{\sqrt{3}}{2}z=0\end{cases}$，

取$z=\sqrt{3}$，得$y=1$，$x=\dfrac{1}{2}$，

则平面$AEF$的一个法向量$\boldsymbol {n}=\left(\dfrac{1}{2},1,\sqrt{3}\right)$，

故$\overrightarrow{BG}\cdot \boldsymbol {n}=0\times \dfrac{1}{2}-\dfrac{3}{4}\times 1+\dfrac{\sqrt{3}}{4}\times \sqrt{3}=0$，

则$\overrightarrow{BG}\perp \boldsymbol {n}$．且$BG\not\subset$平面$AEF$，

则$BG//$平面$AEF$．

$(2)$设$\overrightarrow{CP}=\lambda \overrightarrow{CF},\lambda \in (0,1)$，设$P(a,b,c)$，

$\because C\left(0,-\dfrac{1}{2},0\right)$，$F\left(0,0,\dfrac{\sqrt{3}}{2}\right)$，

$\therefore \left(a,b+\dfrac{1}{2},c\right)=\lambda \left(0,\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)$，于是有$P\left(0,\dfrac{1}{2}\lambda -\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\lambda \right)$，

$\therefore \overrightarrow{BP}=\left(0,\dfrac{1}{2}\lambda -1,\dfrac{\sqrt{3}}{2}\lambda \right)$，

又$\overrightarrow{BD}=(2,-1,0)$．设平面$BDP$法向量$\boldsymbol {{n}_{1}}=(x,y,z)$，

则$\begin{cases}{\boldsymbol {{n}_{1}}\perp \overrightarrow{BD}}\\ {\boldsymbol {{n}_{1}}\perp \overrightarrow{BP}}\end{cases}$，则$\begin{cases}\boldsymbol {{n}_{1}}\cdot \overrightarrow{BD}=0\\ \boldsymbol {{n}_{1}}\cdot \overrightarrow{BP}=0\end{cases}$，即$\left\{ \begin{align} & 2x-y=0 \\ & (\frac{\lambda }{2}-1)y+\frac{\sqrt{3}}{2}\lambda z=0 \\ \end{align} \right.$，

$\therefore $ 平面$BDP$的一个法向量为$\boldsymbol {n}_{1}=\left(1,2,\dfrac{2(2-\lambda )}{\sqrt{3}\lambda }\right)$，

平面$BCF$的一个法向量为$\boldsymbol {{n}_{2}}=(1,0,0)$，

则$\vert \cos \lt \boldsymbol {{n}_{1}},\boldsymbol {{n}_{2}}\gt \vert =\dfrac{\vert \boldsymbol {{n}_{1}}\cdot \boldsymbol {{n}_{2}}\vert }{\vert \boldsymbol {{n}_{1}}\vert \cdot \vert \boldsymbol {{n}_{2}}\vert }=\dfrac{1}{\sqrt{5+\dfrac{4(2-\lambda )^{2}}{3{\lambda }^{2}}}}=\cos 6{0}^\circ =\dfrac{1}{2}$，

化简得$\dfrac{4(2-\lambda )^{2}}{3{\lambda }^{2}}=-1$，

$\therefore \lambda$无实数解，不存在这样的点$P$．