如图，圆柱$OO_{1}$的底面半径和母线长均为$3$，$AB$是底面直径，点$C$在圆$O$上且$OC\perp AB$，点$E$在母线$BD$上，$BE=2$，点$F$是上底面的一个动点，则$(\qquad)$．

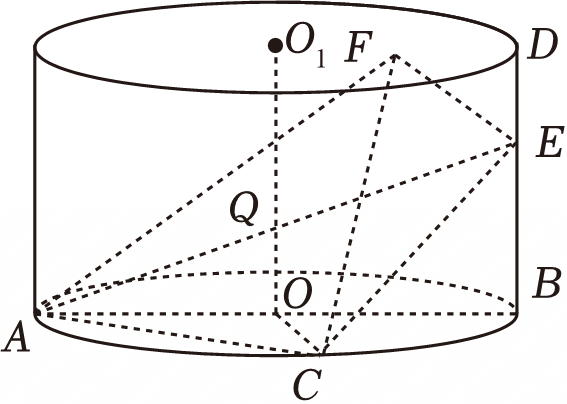
存在唯一的点$F$，使得$AF+FE=2\\sqrt{13}$

若$AE\\perp CF$，则点$F$的轨迹长为$4$

若$AF\\perp FE$，则四面体$ACEF$的外接球的表面积为$40\\pi$

若$AF\\perp FE$，则点$F$的轨迹长为$2\\sqrt{6}\\pi$

设$E$关于$D$点的对称点为$E'$，如图，

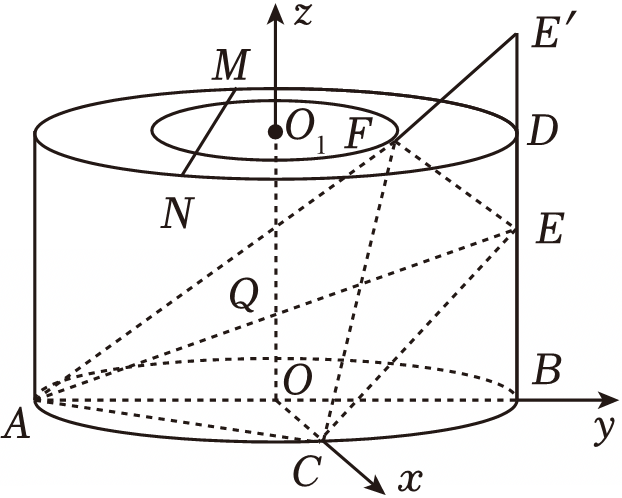
则$AF+EF=AF+FE'\geqslant AE'=\sqrt{A{B^2}+B{{E'}^2}}=\sqrt{{6^2}+{4^2}}=2\sqrt{13}$，

$\therefore AF+FE\geqslant 2\sqrt{13}$，当且仅当$A$，$F$，$E'$三点共线时取等号，

故存在唯一的点$F$，使得$AF+FE=2\sqrt{13}$，故$\rm A$正确；

由题意知$OC\perp AB$，$OO_{1}\perp OC$，$OO_{1}\perp AB$，

以$O$为坐标原点，以$OC$，$OB$，$OO_{1}$为$x$，$y$，$z$轴的正方向，建建系如图，

则$A(0,-3,0)$，$C(3,0,0)$，$E(0,3,2)$，设$F(x,y,3)$，

则$\overrightarrow{AE}=(0,6,2)$，$\overrightarrow{CF}=(x-3,y,3)$，$\overrightarrow{AF}=(x,y+3,3)$，$\overrightarrow{FE}=(x,y-3,1)$，

对选项$\rm B$：当$AE\perp CF$时，$\overrightarrow{AE}\cdot \overrightarrow{CF}=6y+6=0$，

$\therefore y=-1$，

$\therefore $ 点$F$的轨迹长为上底面圆$O_{1}$的一条弦$MN$，$O_{1}$到$MN$的距离为$1$，

$\therefore MN=2\sqrt{{3^2}-1}=4\sqrt{2}$，故点$F$的轨迹长为$4\sqrt{2}$，

$\therefore \rm B$错误；

对选项$\rm D$：当$AF\perp FE$时，$\overrightarrow{AF}\cdot \overrightarrow{FE}=(x,y+3,3)\cdot (x,y-3,1)=0$，

$\therefore x^{2}+y^{2}=6$，

$\therefore $ 点$F$的轨迹是以$O_{1}$为圆心，$\sqrt{6}$为半径的圆，其轨迹长为$2\sqrt{6}\pi$，故$\rm D$正确；

对选项$\rm C$：在$\triangle ACE$中，$AC=3\sqrt{2}$，$CE=\sqrt{{{(3\sqrt{2})}^2}+{2^2}}=\sqrt{22}$，$AE=\sqrt{{6^2}+{2^2}}=\sqrt{40}$，

$\therefore AC^{2}+CE^{2}=AE^{2}$，

$\therefore \triangle ACE$为直角三角形，其外心为$AE$与$OO_{1}$的交点$Q$，且$OQ=1$，$QE=\sqrt{10}$，

而$QF=\sqrt{Q{ O}_1^2+{O_1}{F^2}}=\sqrt{{2^2}+6}=\sqrt{10}$，

$\therefore QF=QE=QC=QA$，

$\therefore Q$为四面体$ACEF$的外接球的球心，球半径为$\sqrt{10}$，

$\therefore $ 球的表面积为$40\pi$，故$\rm C$正确．

故选：$\rm ACD$