在如图$1$所示的图形中，四边形$ABCD$为菱形，$\angle BAD=60^\circ$，$\triangle $$PAD$和$\triangle $$BCQ$均为直角三角形，$\angle PDA=\angle QCB=90^\circ$，$PD=AD=2CQ=2$，现沿$AD$，$BC$将$\triangle $$PAD$和$\triangle $$BCQ$进行翻折，使$PD//QC$（$PD$，$QC$在平面$ABCD$同侧），如图$2$．

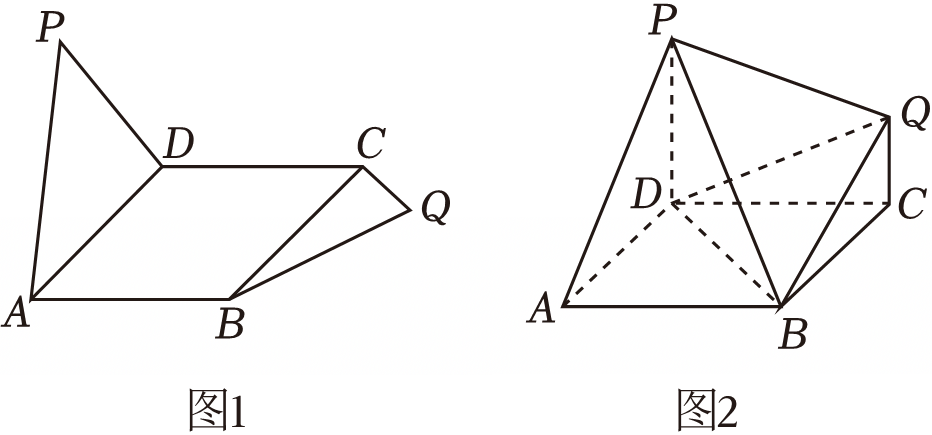
$(1)$当二面角$P-AD-B$为$90^\circ$时，判断$DQ$与平面$PAB$是否平行；

$(2)$探究当二面角$P-AD-B$为$120^\circ$时，平面$PBQ$与平面$PBD$是否垂直；

$(3)$在$(2)$的条件下，求平面$PBD$与平面$QBC$夹角的余弦值．

$(1)$$DQ$不与平面$PAB$平行；

$(2)$平面$PBQ$不与平面$PBD$垂直；

$(3)$$\\dfrac{2\\sqrt{13}}{13}$

$(1)$若二面角$P-AD-B$为$90^\circ$，则平面$PAD\perp$平面$ABCD$，

$\because $ 平面$PAD\cap$平面$ABCD=AD$，且$PD\perp AD$，

$\therefore PD\perp$平面$ABCD$，

如图，以$D$为坐标原点，$\overrightarrow{DA}$，$\overrightarrow{DP}$的方向分别为$x$，$z$轴的正方向，建立空间直角坐标系，

则$P(0,0,2)$，$D(0,0,0)$，$B(1,\sqrt{3},0)$，$Q(-1,\sqrt{3},1)$，$A(2,0,0)$，

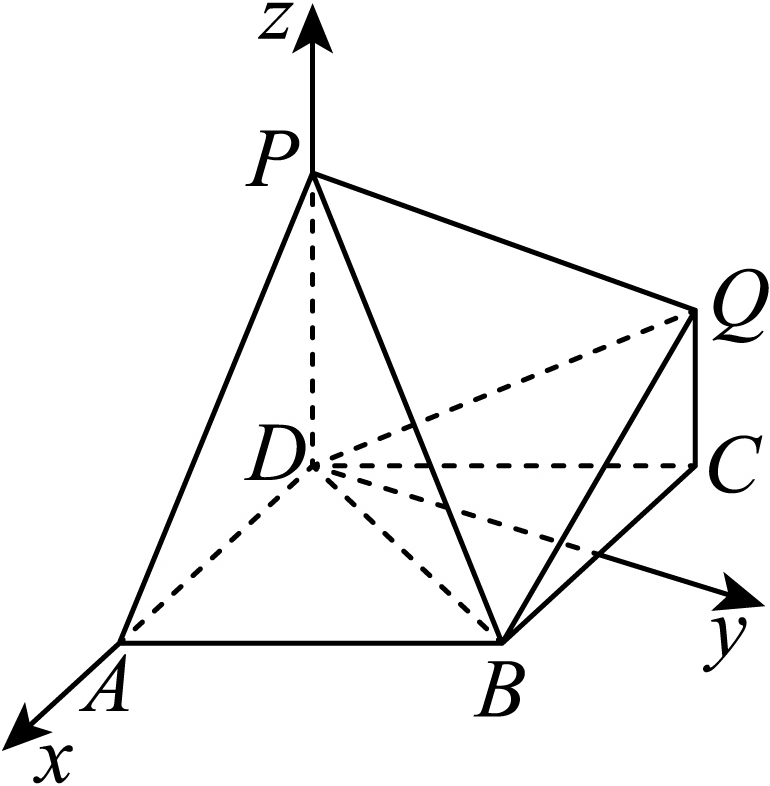
设平面$PAB$的法向量为$\boldsymbol{n}=(x,y,z)$，

$\because \overrightarrow{BP}=(-1,-\sqrt{3},2)$，$\overrightarrow{BA}=(1,-\sqrt{3},0)$，

$\therefore \left\{\begin{array}{l}\boldsymbol{n}\cdot \overrightarrow{BP}=-x-\sqrt{3}y+2z=0\\ \boldsymbol{n}\cdot \overrightarrow{BA}=x-\sqrt{3}y=0\end{array}\right.$

令$x=3$，得$\boldsymbol{n}=(3,\sqrt{3},3)$，

$\because \overrightarrow{DQ}=(-1,\sqrt{3},1)$，

$\therefore\overrightarrow{DQ}\cdot\boldsymbol{n}=-1\times3+\sqrt{3}\times\sqrt{3}+1\times3\ne0$，

$\therefore DQ$不与平面$PAB$平行．

$(2)$取$BC$的中点$E$，连接$DE$，则$DE\perp AD$，

$\because AD\perp PD$，

$\therefore $ 二面角$P-AD-B$的平面角为$\angle PDE$，即$\angle PDE=120^\circ$，

如图，以$D$为坐标原点，$\overrightarrow{DA}$，$\overrightarrow{DE}$的方向分别为$x$，$y$轴的正方向，建立空间直角坐标系，

则$P(0,-1,\sqrt{3})$，$D(0,0,0)$，$B(1,\sqrt{3},0)$，$Q\left(-1,\sqrt{3}-\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)$，

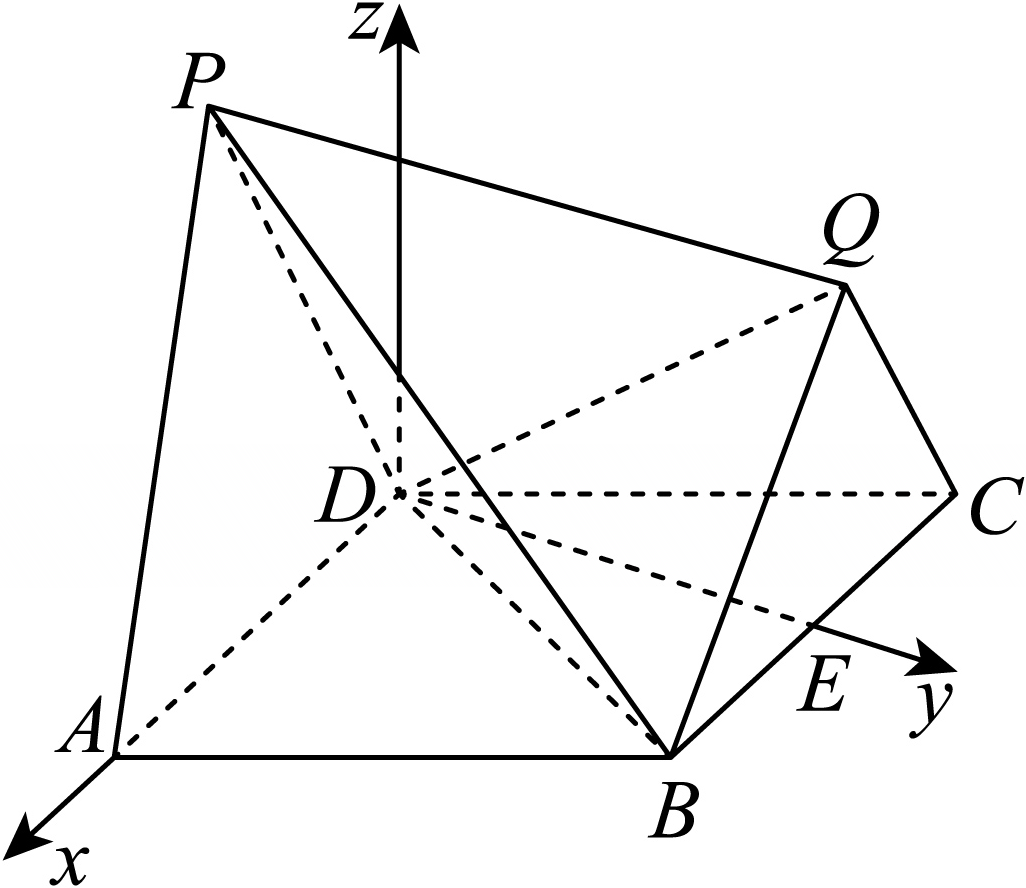
设平面$PBD$的法向量为$\boldsymbol{m}=(x_{1},y_{1},z_{1})$，

$\because \overrightarrow{DB}=(1,\sqrt{3},0)$，$\overrightarrow{DP}=(0,-1,\sqrt{3})$，

$\therefore \left\{\begin{array}{l}\boldsymbol{m}\cdot \overrightarrow{DB}={x}_{1}+\sqrt{3}{y}_{1}=0,\\ \boldsymbol{m}\cdot \overrightarrow{DP}=-{y}_{1}+\sqrt{3}{z}_{1}=0,\end{array}\right.$令$z_{1}=1$，得$\boldsymbol{m}=(-3,\sqrt{3},1)$，

设平面$PBQ$的法向量为$\boldsymbol{n}=(x_{2},y_{2},z_{2})$，

$\because \overrightarrow{BP}=(-1,-\sqrt{3}-1,\sqrt{3})$，$\overrightarrow{BQ}=\left(-2,-\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)$，

则$\begin{cases}{\boldsymbol{n}\perp \overrightarrow{BP}}\\ {\boldsymbol{n}\perp \overrightarrow{BQ}}\end{cases}$，

$\therefore \left\{\begin{array}{l}\boldsymbol{n}\cdot \overrightarrow{BP}=-{x}_{2}-(\sqrt{3}+1){y}_{2}+\sqrt{3}{z}_{2}=0\\ \boldsymbol{n}\cdot \overrightarrow{BQ}=-2{x}_{2}-\dfrac{1}{2}{y}_{2}+\dfrac{\sqrt{3}}{2}{z}_{2}=0,\end{array}\right.$

令${x}_{2}=\sqrt{3}$，得$\boldsymbol{n}=(\sqrt{3},3,4+\sqrt{3})$，

$\because\boldsymbol{m}\cdot\boldsymbol{n}=4+\sqrt{3}\ne0$，

$\therefore \boldsymbol{m}$，$\boldsymbol{n}$不垂直，

$\therefore $ 平面$PBQ$不与平面$PBD$垂直．

$(3)$在$(2)$中的坐标系中，设平面$QBC$的法向量为$\boldsymbol{p}=(x,y,z)$，

$\because \overrightarrow{BC}=(-2,0,0)$，$\overrightarrow{BQ}=\left(-2,-\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)$，

则$\begin{cases}{\boldsymbol{p}\perp \overrightarrow{BC}}\\ {\boldsymbol{p}\perp \overrightarrow{BQ}}\end{cases}$，

$\therefore \left\{\begin{array}{l}\boldsymbol{p}\cdot \overrightarrow{BC}=-2x=0,\\ \boldsymbol{p}\cdot \overrightarrow{BQ}=-2x-\dfrac{1}{2}y+\dfrac{\sqrt{3}}{2}z=0,\end{array}\right.$

令$z=1$，得$\boldsymbol{p}=(0,\sqrt{3},1)$，

设平面$PBD$与平面$QBC$的夹角为$\theta$，

则$\cos\theta=|\cos\langle\boldsymbol{m},\boldsymbol{p}\rangle|=\dfrac{|\boldsymbol{m}\cdot\boldsymbol{p}|}{|\boldsymbol{m}||\boldsymbol{p}|}=\dfrac{4}{2\sqrt{13}}=\dfrac{2\sqrt{13}}{13}$，

$\therefore $ 平面$PBD$与平面$QBC$夹角的余弦值为$\dfrac{2\sqrt{13}}{13}$．