如图，直三棱柱$ABC$一$A_{1}B_{1}C_{1}$中，侧棱长为$2$，$AC=BC=1$，$\angle ACB=90^{\circ}$，$D$是$A_{1}B_{1}$的中点，$F$是$BB_{1}$上的动点，$AB_{1}$，$DF$交于点$E$，要使$AB_{1}\bot $平面$C_{1}DF$，则线段$B_{1}F$的长为                  .

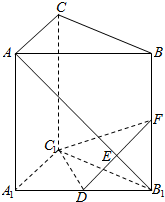
以$C_{1}$为原点，$C_{1}A_{1}$为$x$轴，$C_{1}B_{1}$为$y$轴，$C_{1}C$为$z$轴，建立空间直角坐标系，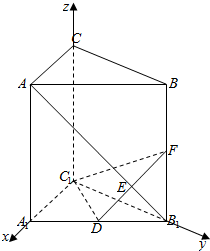
由题意$A_{1}(1,0,0)$，$B_{1}(0,1,0)$，$D(\dfrac{1}{2},\dfrac{1}{2}$，$0)$，$C_{1}(0,0,0),A\left(1,0,2\right)$，设$F\left(0,1,t\right)$，$0\leqslant t\leqslant 2$，
$\overrightarrow{{C}_{1}D}=(\dfrac{1}{2},\dfrac{1}{2}$，$0)$，$\overrightarrow{A{B}_{1}}=\left(-1,1,-2\right)$，$\overrightarrow{{{C}_{1}F}}=\left(0,1,t\right)$，
$\because AB_{1}\bot $平面$C_{1}DF$，
$\therefore \left\{\begin{array}{l}{\overrightarrow{A{B}_{1}}\cdot \overrightarrow{{C}_{1}D}=0}\\{\overrightarrow{A{B}_{1}}\cdot \overrightarrow{{C}_{1}F}=0}\end{array}\right.$，$\therefore 1-2t=0$，解得$t=\dfrac{1}{2}$.
$\therefore $线段$B_{1}F$的长为$\dfrac{1}{2}$.
故答案为：$\dfrac{1}{2}$.