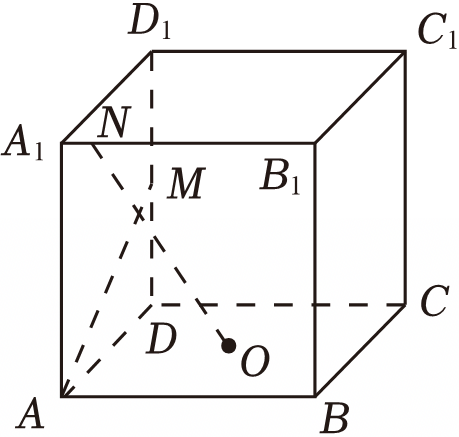
如图，在棱长为$6$的正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$O$是底面正方形$ABCD$的中心，点$M$在$DD_{1}$上，点$N$在$A_{1}B_{1}$上，若$ON\perp AM$，则$DM=(\qquad)$．

$1$

$2$

$4$

$3$

以点$D$为坐标原点，$DA$、$DC$、$DD_{1}$所在直线分别为$x$、$y$、$z$轴建立空间直角坐标系，

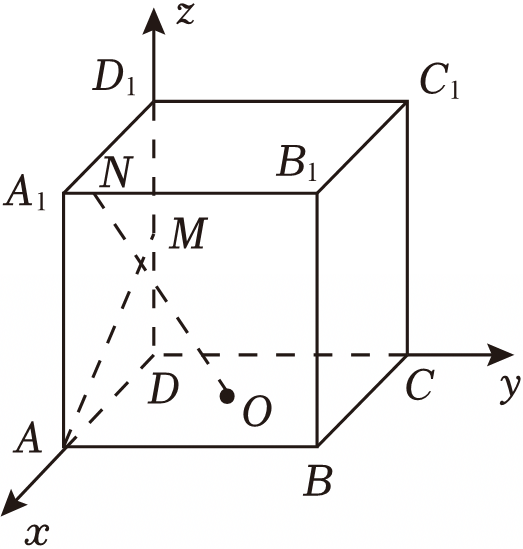
则$A(6,0,0)$、$O(3,3,0)$，设点$N(6,n,6)$，$M(0,0,m)$，其中$N(6,n,6)$，$M(0,0,m)$，

$\overrightarrow{AM}=(-6,0,m)$，$\overrightarrow{ON}=(3,n-3,6)$，

$\because ON\perp AM$，则$\overrightarrow{ON}\cdot \overrightarrow{AM}=3\times (-6)+6m=0$，解得$m=3$，故$DM=3$．

故选：$\rm D$