一副三角板如图拼接，将$\triangle BCD$折起，使得二面角$A-BC-D$为直二面角，求证：平面$ABD\bot $平面$ACD$.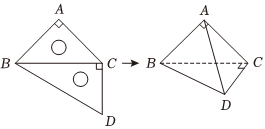

证明见解析

证明：如图所示，取$BC$的中点$O$，连接$OA$，过点$O$作$CD$的平行线，交$BD$于点$E$，

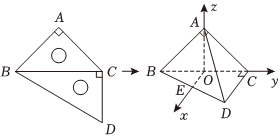
$\because AB=AC$，$\therefore AO\bot BC$，
$\because $二面角$A-BC-D$为直二面角，$\therefore AO\bot $平面$BCD$.
$\therefore AO\bot OE$，$AO\bot OC$，
又$CD\bot BC,OE$∥$CD$，
$\therefore OC\bot OE$.
建立空间直角坐标系$O-xyz.O\left(0,0,0\right)$.
设$CD=2$，则$C(0$，$\sqrt{3}$，$0)$，$D(2$，$\sqrt{3}$，$0)$，$A(0$，$0$，$\sqrt{3}$），$B(0$，$-\sqrt{3}$，$0)$.
$\overrightarrow{DA}=(-2$，$-\sqrt{3}$，$\sqrt{3}$），$\overrightarrow{CD}=\left(2,0,0\right)$，$\overrightarrow{BD}=(2$，$2\sqrt{3}$，$0)$.
设平面$ACD$的法向量$\boldsymbol{m}=\left(x,y,z\right)$.则$\boldsymbol{m}\cdot \overrightarrow{DA}=\boldsymbol{m}\cdot \overrightarrow{CD}=0$，$\therefore -2x-\sqrt{3}y+\sqrt{3}z=0$，$2x=0$，
取$\boldsymbol{m}=\left(0,1,1\right)$.
同理可得：平面$ABD$的法向量$\boldsymbol{n}=(\sqrt{3}$，$-1,1)$.
$\therefore \boldsymbol{m}\cdot \boldsymbol{n}=0-1+1=0$.
$\therefore \boldsymbol{m}\bot \boldsymbol{n}$.
$\therefore $平面$ABD\bot $平面$ACD$.