在《九章算术$\cdot$商功》中将上、下底面均为正方形的正棱台称为方亭，在方亭$ABCD-A_{1}B_{1}C_{1}D_{1}$中，$AB=2A_{1}B_{1}=4$，方亭的体积为$\dfrac{28}{3}$，则侧面$ABB_{1}A_{1}$的面积为$(\qquad)$．

$3\\sqrt{2}$

$\\sqrt{7}$

$2\\sqrt{2}$

$3\\sqrt{11}$

设方亭的高为$h$，

$\because AB=2A_{1}B_{1}=4$，方亭的体积为$\dfrac{28}{3}$，

$\therefore V=\dfrac{1}{3}(2^2+4^2+\sqrt{2^2\times 4^2})\times h=\dfrac{28}{3}$，解得$h=1$，如图，

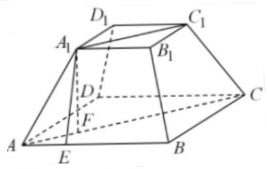
过$A_{1}$作$A_{1}E\perp AB$，垂足为$E$，连接$AC$，$A_{1}C_{1}$，过$A_{1}$作$A_{1}F\perp AC$，垂足为$F$，

易知四边形$ACC_{1}A_{1}$ 为等腰梯形，且$AC=4\sqrt{2}$，$A_1C_1=2\sqrt{2}$，$AF=\sqrt{2}$，$AE=1$，$AA_1=\sqrt{{\rm A}_1F^2+AF^2}=\sqrt{3}$，

$\because $ 侧面$ABB_{1}A_{1}$为等腰梯形，

$\therefore A_1E=\sqrt{A{\rm A}_1^2-AE^2}=\sqrt{3-1}=\sqrt{2}$，

$\therefore $ 侧面$ABB_{1}A_{1}$的面积为$\dfrac{1}{2}(AB+A_1B_1)\cdot A_1E=3\sqrt{2}$．

故选：$\rm A$