| 4.2.3 二项分布与超几何分布 题目答案及解析
稿件来源:高途
| 4.2.3 二项分布与超几何分布题目答案及解析如下,仅供参考!
选择性必修二
第四章 概率与统计
4.2 随机变量
4.2.3 二项分布与超几何分布
某市为提升中学生的环境保护意识,举办了一次“环境保护知识竞赛”,分预赛和复赛两个环节,预赛成绩排名前三百名的学生参加复赛.已知共有$12000$名学生参加了预赛,现从参加预赛的全体学生中随机地抽取$100$人的预赛成绩作为样本,得到如右频率分布直方图:
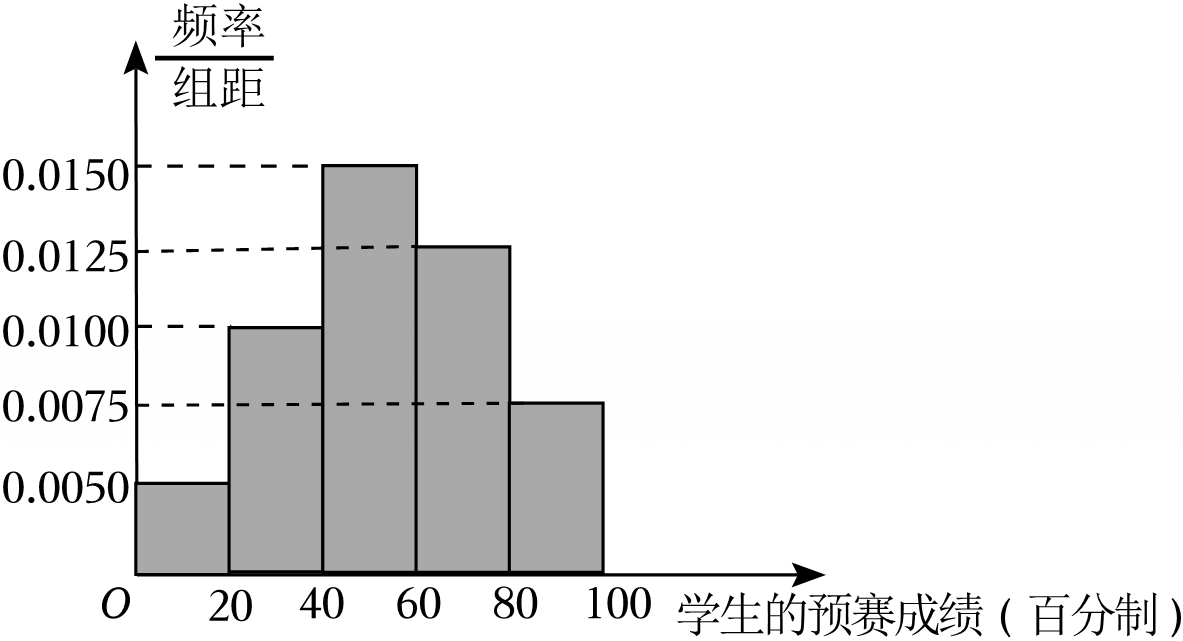
$(1)$规定预赛成绩不低于$80$分为优良,若从上述样本中预赛成绩不低于$60$分的学生中随机地抽取$2$人,求至少有$1$人预赛成绩优良的概率,并求预赛成绩优良的人数$X$的分布列及数学期望;
$(2)$由频率分布直方图可认为该市全体参加预赛学生的预赛成绩$Z$服从正态分布$N(\mu ,\sigma ^{2})$,其中$\mu$可近似为样本中的$100$名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且$\sigma ^{2}=362$,已知小明的预赛成绩为$91$分,利用该正态分布,估计小明是否有资格参加复赛?
附:若$Z\sim N(\mu ,\sigma ^{2})$,则$P(\mu -\sigma \lt Z\lt \mu +\sigma )\approx 0.6827$,$P(\mu -2\sigma \lt Z\lt \mu +2\sigma )\approx 0.9545$,$P(\mu -3\sigma \lt Z\lt \mu +3\sigma )\approx 0.9973$;$\sqrt{362}\approx 19$.
$(1)\\dfrac{8}{13}$,
分布列为:
| $X$ | $0$ | $1$ | $2$ |
| $P$ | $\\dfrac{5}{13}$ | $\\dfrac{25}{52}$ | $\\dfrac{7}{52}$ |
$E(X)=\\dfrac{3}{4}$;
$(2)$有资格参加复赛.
"]]$(1)$由题预赛成绩在$60$,$80)$范围内的样本量为:$0.0125\times 20\times 100=25$,
预赛成绩在$[80,100]$范围内的样本量为:$0.0075\times 20\times 100=15$,
设抽取的$2$人中预赛成绩优良的人数为$x$,可能取值为$0$,$1$,$2$,
$\therefore P(X\geqslant 1)=\dfrac{{\rm C}_{1}^{1}{\rm C}_{25}^{1}+{\rm C}_{15}^{2}{\rm C}_{25}^{0}}{{\rm C}_{40}^{2}}=\dfrac{8}{13}$,
又$P(X=0)=\dfrac{{\rm C}_{25}^{2}}{{\rm C}_{40}^{2}}=\dfrac{5}{13}$,$P(X=1)=\dfrac{\rm C_{25}^{1}{\rm C}_{15}^{1}}{{\rm C}_{40}^{2}}=\dfrac{25}{52}$,$P(X=2)=\dfrac{\rm C_{15}^{2}}{{\rm C}_{40}^{2}}=\dfrac{7}{52}$,
则$X$的分布列为:
| $X$ | $0$ | $1$ | $2$ |
| $P$ | $\dfrac{5}{13}$ | $\dfrac{25}{52}$ | $\dfrac{7}{52}$ |
故$E(X)=0\times \dfrac{5}{13}+1\times \dfrac{25}{52}+2\times \dfrac{7}{52}=\dfrac{3}{4}$;
$(2)$由题$\mu =\overline{x}=(10\times 0.005+30\times 0.01+50\times 0.015+70\times 0.0125+90\times 0.0075)\times 20=53$,又$\delta ^{2}=362$,
则$\delta \approx 19$,$Z\sim N(53,362)$,
$\therefore P(Z\geqslant 91)=P(Z\geqslant \mu +2\sigma )=[1-P(\mu -2a\lt Z\lt \mu +2\sigma )]\approx 0.02275$,
故全市参加预赛学生中,成绩不低于$91$分的有$12000\times 0.02275=273$人,
$\because 273\lt 300$,故小明有资格参加复赛.
| 4.2.3 二项分布与超几何分布题目答案及解析(完整版)
