| 4.2.2 离散型随机变量的分布列 题目答案及解析
稿件来源:高途
| 4.2.2 离散型随机变量的分布列题目答案及解析如下,仅供参考!
选择性必修二
第四章 概率与统计
4.2 随机变量
4.2.2 离散型随机变量的分布列
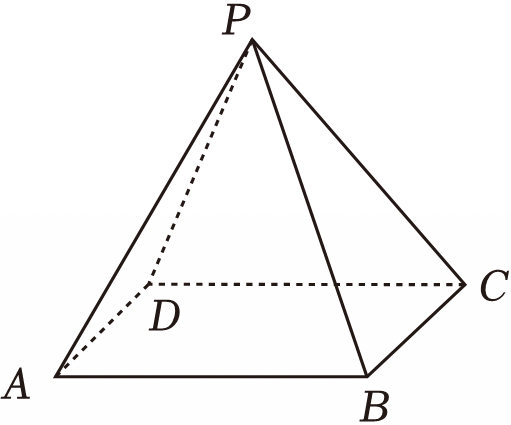
已知正四棱锥$P-ABCD$的底面边长和高都为$2$.现从该棱锥的$5$个顶点中随机选取$3$个点构成三角形,设随机变量$X$表示所得三角形的面积.
$(1)$求概率$P(X=2)$的值;
$(2)$求随机变量$X$的概率分布及其数学期望$E(X)$.
$(1)$$\\dfrac{2}{5}$;
$(2)$随机变量$X$的概率分布列为:
| $X$ | $\\sqrt{5}$ | $2$ | $2\\sqrt{2}$ |
| $P(X)$ | $\\dfrac{2}{5}$ | $\\dfrac{2}{5}$ | $\\dfrac{1}{5}$ |
$E(X)=\\dfrac{2\\sqrt{5}+2\\sqrt{2}+4}{5}$.
"]]$(1)$从$5$个顶点中随机选取$3$个点构成三角形,共有${\rm C}_5^3=10$种取法,
其中$X=2$的三角形如$\triangle ABD$,这类三角形共有${\rm C}_4^3=4$个,
因此$P(X=2)=\dfrac{4}{10}=\dfrac{2}{5}$;
$(2)$由题意,$X$的可能取值为$\sqrt{5},2,2\sqrt{2}$,
其中$X=\sqrt{5}$的三角形是侧面,这类三角形共有$4$个,
其中$X=2\sqrt{2}$的三角形有两个,$\triangle PAC$和$\triangle PBD$,
因此$P(X=\sqrt{5})=\dfrac{2}{5},P(X=2\sqrt{2})=\dfrac{1}{5}$,
$\therefore $ 随机变量$X$的概率分布列为:
| $X$ | $\sqrt{5}$ | $2$ | $2\sqrt{2}$ |
| $P(X)$ | $\dfrac{2}{5}$ | $\dfrac{2}{5}$ | $\dfrac{1}{5}$ |
所求数学期望$E(X)=\sqrt{5}\times \dfrac{2}{5}+2\times \dfrac{2}{5}+2\sqrt{2}\times \dfrac{1}{5}=\dfrac{2\sqrt{5}+2\sqrt{2}+4}{5}$.
| 4.2.2 离散型随机变量的分布列题目答案及解析(完整版)
