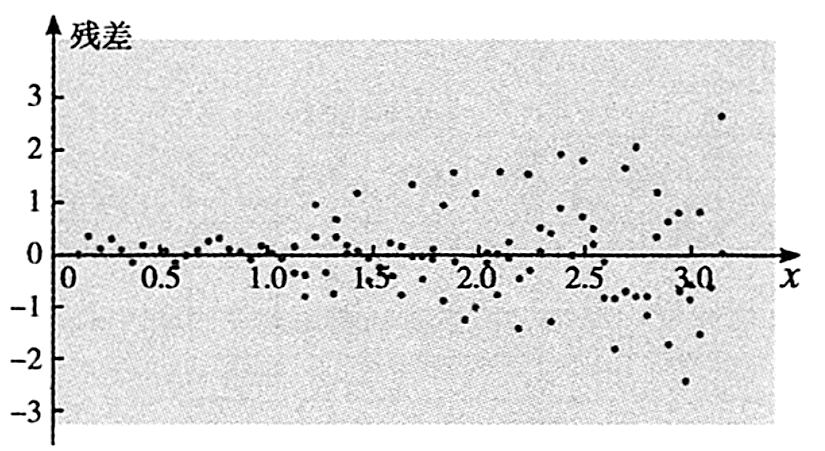
对于变量$Y$和变量$x$的成对样本观测数据，用一元线性回归模型$\begin{cases} Y=bx+a+e \\ E(e)=0,D(e)={{\sigma }^{2}} \\ \end{cases}$得到经验回归模型$\hat{y}=\hat{b} x+\hat{a}$，对应的残差如下图所示，模型误差$(\qquad)$

满足一元线性回归模型的所有假设

不满足一元线性回归模型的$E(e)=0$的假设

不满足一元线性回归模型的$D(e)={{\\sigma }^{2}}$假设

不满足一元线性回归模型的$E(e)=0$和$D(e)={{\\sigma }^{2}}$的假设

用一元线性回归模型$\begin{cases} Y=bx+a+e \\ E(e)=0,D(e)={{\sigma }^{2}} \\ \end{cases}$得到经验回归模型$\hat{y}=\hat{b} x+\hat{a}$，根据对应的残差图，残差的均值$E(e)=0$可能成立，但明显残差的$x$轴上方的数据更分散，$D(e)={{\sigma }^{2}}$不满足一元线性回归模型，正确的只有$C$.

故选：$\rm C$