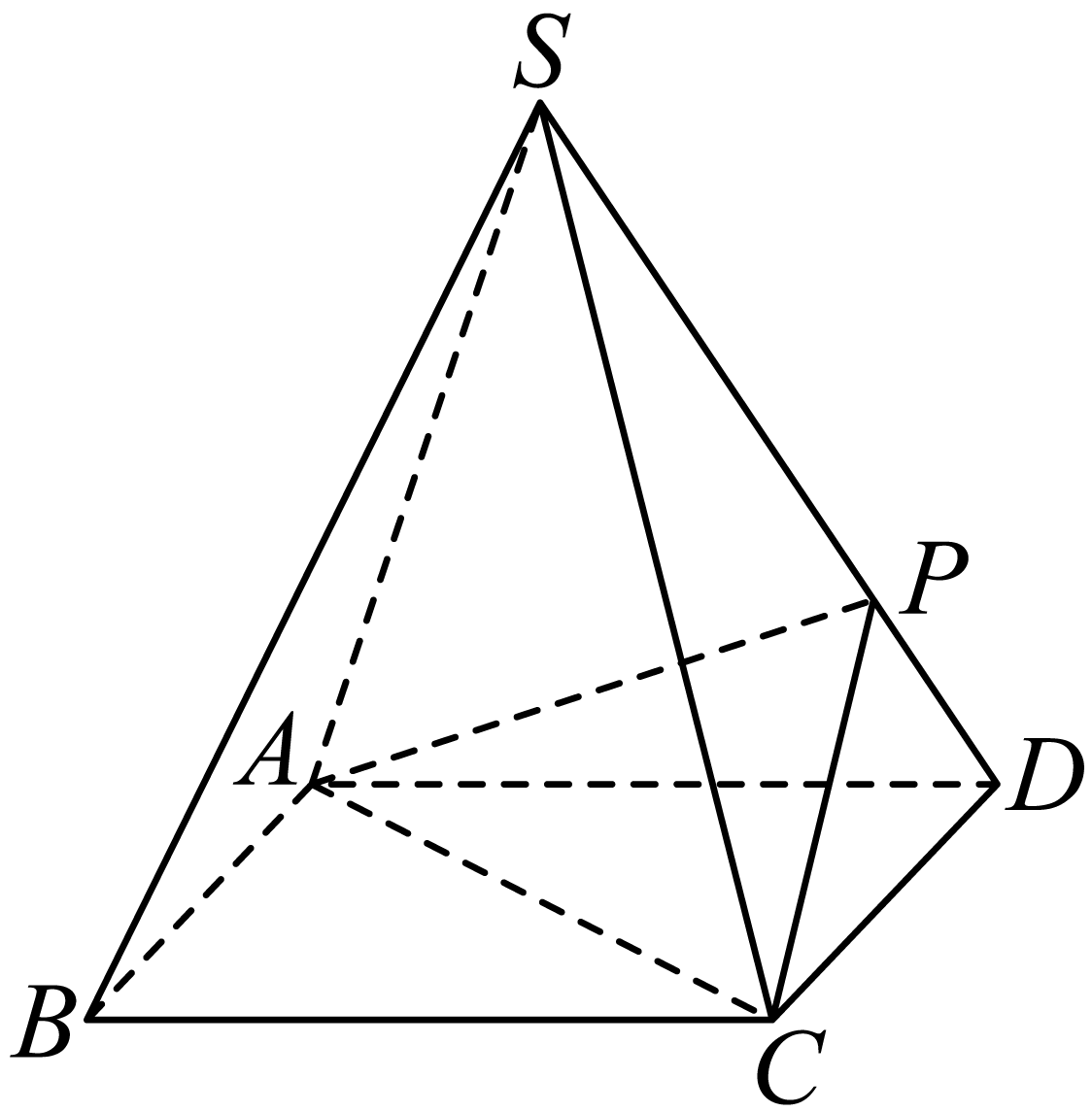
如图所示，四棱锥$S-ABCD$的底面是正方形，每条侧棱的长都是底面边长的$\sqrt{2}$倍，$P$为侧棱$SD$上的点．  

$(1)$求证：$AC⊥SD$；

$(2)$若$SD$$\perp $平面$PAC$，则侧棱$SC$上是否存在一点$E$，使得$BE//$平面$PAC$？若存在，求$SE$∶$EC$的值；若不存在，试说明理由．

$(1)$证明见解析

$(2)$$SE:EC=2:1$

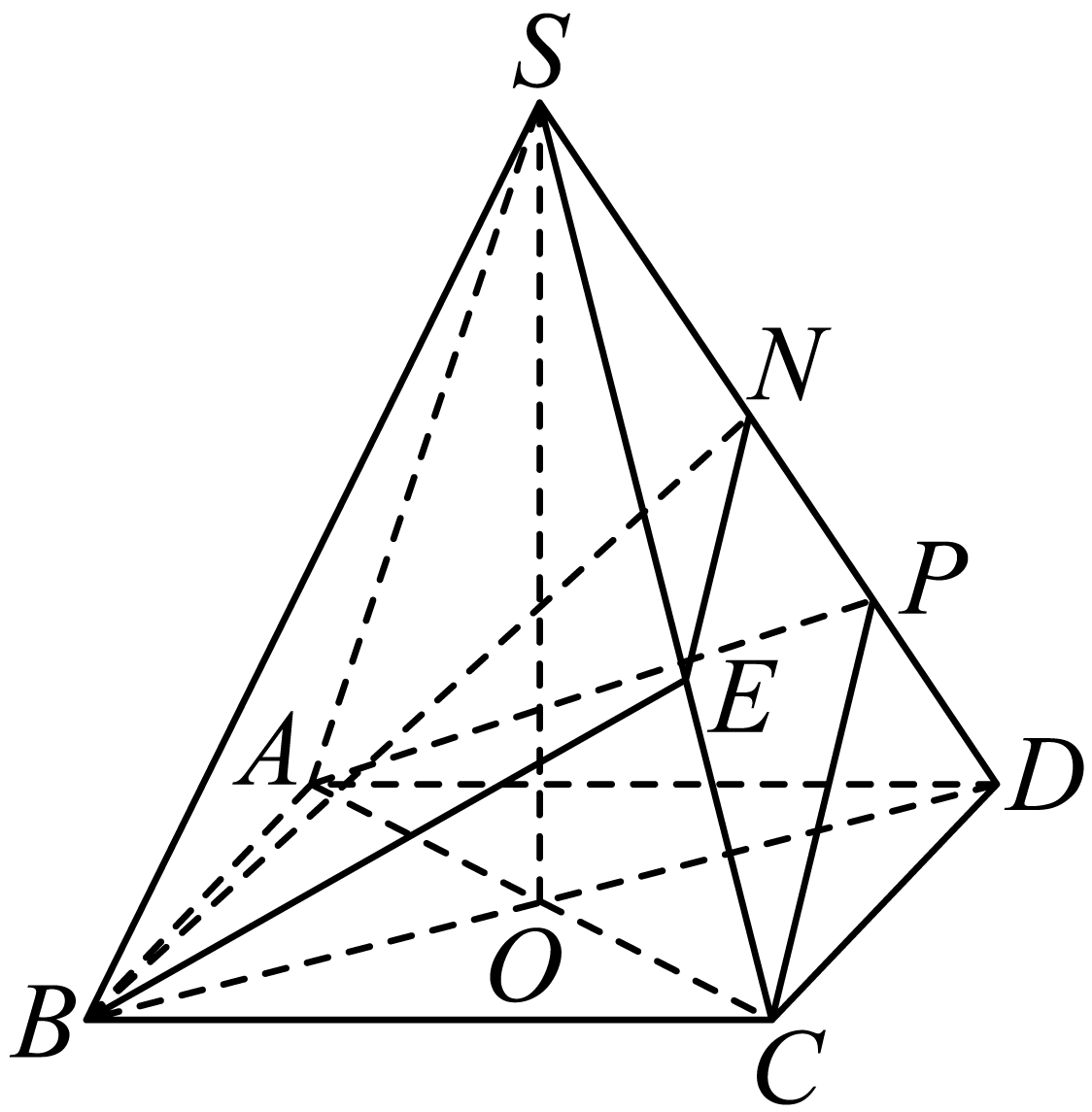
$(1)$连接$AC$，$BD$得交点$O$，连接$SO$，则点$O$是正方形$ABCD$的中心，

$\because SA=SC$，$\triangle S A C$ 是等腰三角形，$SO\perp AC$，

又$AC\perp BD$ ，$BD\subset $ 平面$SBD$，$SO\subset $ 平面$SBD$，$BD\cap SO=O$ ，

$\therefore AC\perp $ 平面$SBD$，$SD\subset $ 平面$SBD$，

$∴$ $AC\perp SD$ ；

$(2)$在$SP$上取点$N$，使得$PN=PD$，过$N$作$NE//PC$交$SC$于点$E$，连$BN$，

由$SD\perp $面$PAC$，$OP\subset $面$PAC$，则$SD\perp OP$，

设底面边长为$a$，则$SD=\sqrt{2}a$，$OD=\dfrac{\sqrt{2}}{2}a$，

$SO=\sqrt{S{{D}^{2}}-O{{D}^{2}}}=\dfrac{\sqrt{6}}{2}a$ ，由等面积法$SO\cdot OD=SD\cdot PO$，得出$PO=\dfrac{\sqrt{6}}{4}a$ ，则$PD=\dfrac{\sqrt{2}}{4}a$ ，

$∵P$是$ND$的中点，$O$是$BD$的中点，

$∴$ $BN//PO$，$PO\subset $面$PAC$，$BN\not\subset $面$PAC$，故$BN//$面$PAC$，

又$NE//PC$，$PC\subset $平面$PAC$，$NE\not\subset $平面$PAC$，

则$NE//$面$PAC$，$BN\cap NE=N$，$BN$，$NE\subset $面$BNE$，

则平面$BNE$$//$平面$PAC$，$BE\subset $面$BNE$，则$BE//$平面$APC$，

$SN=\sqrt{2}a-2\times \dfrac{\sqrt{2}}{4}a=\dfrac{\sqrt{2}}{2}a$ ，$\triangle SNE\sim \triangle SPC$，$SE:EC=SN:NP=\dfrac{\sqrt{2}}{2}a:\dfrac{\sqrt{2}}{4}a=2:1$，

综上，存在，$SE:EC=2:1$．