如图，在四棱锥${{P}-{ABCD}}$中，底面$ABCD$是矩形，$AB=2AD=2$，$PA\perp $平面$ABCD$，$E$为$PD$中点$.$

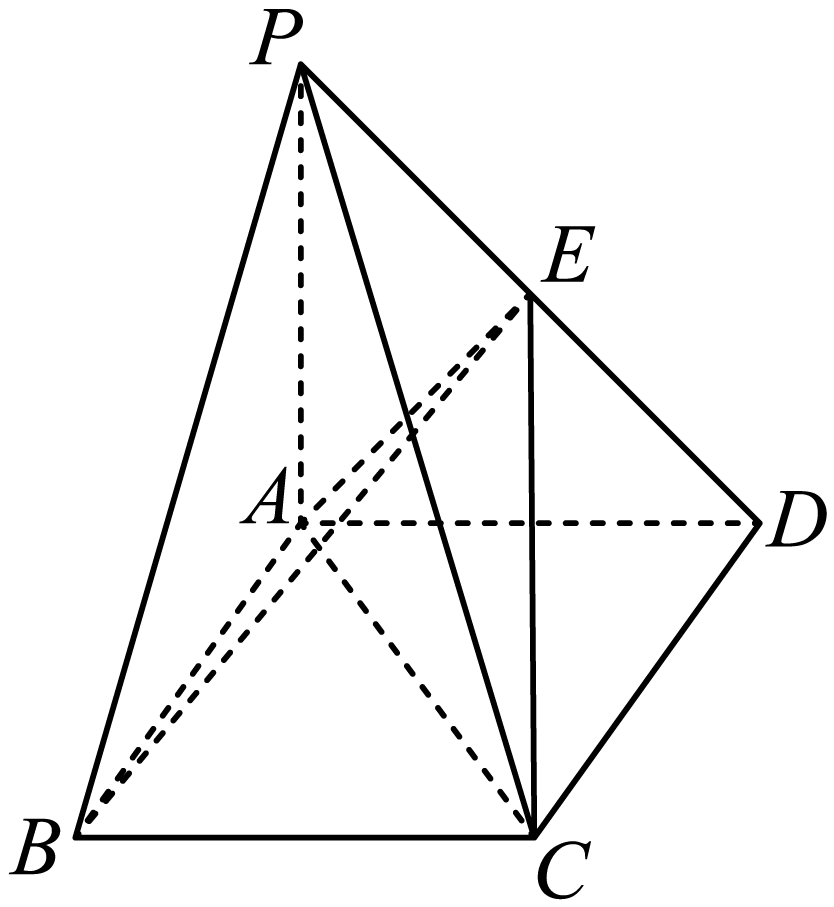
$(1)$若$PA=1$$.$

$(i)$求证：$AE\perp $平面$PCD$；

$(ii)$求直线$BE$与平面$PCD$所成角的正弦值；

$(2)$若平面$BCE$与平面$CED$夹角的正弦值为$\dfrac{\sqrt{21}}{5}$，求$PA.$

$(1)(i)$证明见解析；$(ii)$$\\dfrac{1}{3}$

$(2)2$

$(1)(i)$方法一

$∵$$PA\perp $平面$ABCD$，$CD\subset $平面$ABCD$，$∴$$PA\perp CD$，

$∵$四边形$ABCD$为矩形，$∴$$CD\perp AD$，又$PA\cap AD=A$，$PA$，$A D \subset$平面$PAD$，$∴$$CD\perp $面$PAD$，

$∵$$AE\subset $面$PAD$，$∴$$CD\perp AE$，

在$\triangle PAD$中，$PA=AD=1$，$E$为$PD$中点，$∴$$AE\perp PD$

$∵$$PD\cap CD=D$，$P D \subset$面$PCD$，$CD\subset $面$PCD$，$∴$$AE\perp $平面$PC$  $D$.

方法二：以$A$为原点，$AB$，$AD$，$AP$所在直线分别为$x$轴，$y$轴，$z$轴，建立如图所示的空间直角坐标系，

则$A(0,0,0)$，$B(2,0,0)$，$C(2,1,0)$，$D(0,1,0)$，$P(0,0,1)$，$E\left( 0,\dfrac{1}{2},\dfrac{1}{2} \right)$，

$\overrightarrow{AE}=\left( 0,\dfrac{1}{2},\dfrac{1}{2} \right)$，$\overrightarrow{PC}=(2,1,-1)$，$\because \overrightarrow{AE}\cdot \overrightarrow{PC}=0+\dfrac{1}{2}-\dfrac{1}{2}=0$，$∴$$AE\perp PC$$.$

在$\triangle PAD$中，$PA=AD=1$，$E$为$PD$中点，$∴$$AE\perp PD$$.$

$∵$$PD\cap PC=E$，$P D \subset$面$PCD$，$PC\subset $面$PC$  $D.∴$$AE\perp $平面$PCD$；

方法三：设平面$PCD$的一个法向量为$\boldsymbol{t}=(a,b,c)$，$\overrightarrow{DC}=(1,0,0)$，$\overrightarrow{PD}=(0,1,-1)$，$\overrightarrow{AE}=\left( 0,\dfrac{1}{2},\dfrac{1}{2} \right)$，

则$\begin{cases} \boldsymbol{t}\cdot \overrightarrow{DC}=0 \\ \boldsymbol{t}\cdot \overrightarrow{PD}=0 \\ \end{cases}$，$∴$$\begin{cases} a=0 \\ b-c=0 \\ \end{cases}$$.$

令$b=1$，则$c=1$，$∴$$\boldsymbol{t}=(0,1,1)$，

$\because \overrightarrow{A E}=\dfrac{1}{2} \boldsymbol{t}, \therefore \overrightarrow{A E} \| \boldsymbol{t} \quad \therefore A E \perp$，$∴$$\overrightarrow{AE}//\boldsymbol{t}$，$∴$$AE\perp $平面$PC$  $D$.

$(ii)$由$(i)$得：$AE\perp $平面$PCD$,$PC\subset $平面$PCD$,

$\therefore AE\perp PC$，

在$\triangle PAD$中，$PA=AD=1$，$E$为$PD$中点，

$∴$$AE\perp PD$，$∵$$PD\cap PC=E$，$P D \subset$面$PCD$，$PC\subset $面$PC$  $D$.

$∴$$AE\perp $平面$PCD$，$∴$$\overrightarrow{AE}$为平面$PCD$的一个法向量$\overrightarrow{AE}=\left( 0,\dfrac{1}{2},\dfrac{1}{2} \right)$，$\overrightarrow{B E}=\left(-2, \dfrac{1}{2}, \dfrac{1}{2}\right)$$.$

记直线$BE$与平面$PCD$所成角为$\beta $，

$∴$$\sin \beta =|\cos \langle\overrightarrow{BE}\cdot \overrightarrow{AE}\rangle |=\dfrac{|\overrightarrow{AE}\cdot \overrightarrow{BE}|}{|\overrightarrow{AE}|\cdot |\overrightarrow{BE}|}=\dfrac{\left| \dfrac{1}{4}+\dfrac{1}{4} \right|}{\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}\cdot \sqrt{4+\dfrac{1}{4}+\dfrac{1}{4}}}=\dfrac{1}{3}$，

$∴$直线$BE$与平面$PCD$所成角的正弦值为$\dfrac{1}{3}$；

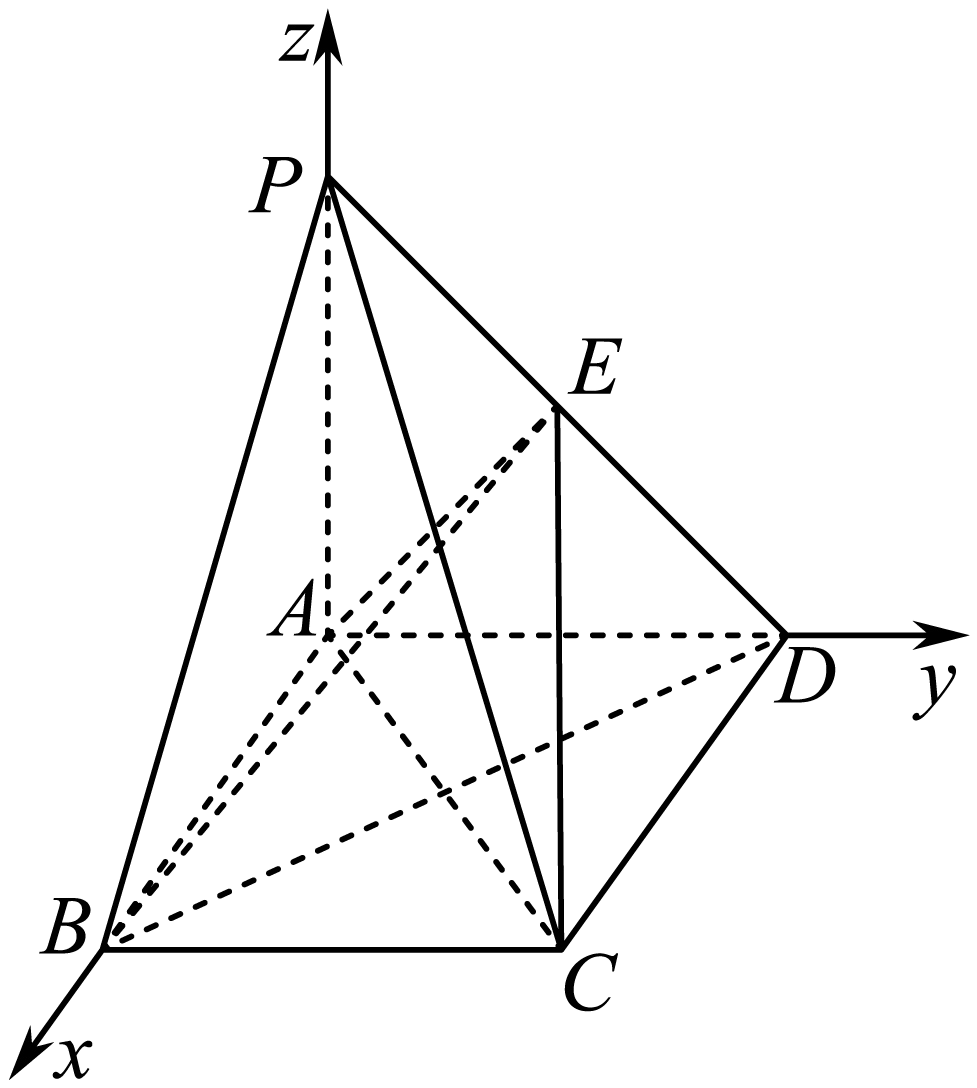
$(2)$设$PA=a(a\gt 0)$，$∴$$\overrightarrow{BC}=(0,1,0)$，$\overrightarrow{AE}=\left( 0,\dfrac{1}{2},\dfrac{a}{2} \right)$，$P A=a(a\gt 0), \therefore \overrightarrow{B C}=(0,1,0), \overrightarrow{A E}=\left(0, \dfrac{1}{2}, \dfrac{a}{2}\right), \overrightarrow{B E}=\left(-2, \dfrac{1}{2}, \dfrac{a}{2}\right)$

设平面$BCE$的一个法向量为$\boldsymbol{n}=(x,y,z)$，

则$\begin{cases} \boldsymbol{n}\cdot \overrightarrow{BC}=0 \\ \boldsymbol{n}\cdot \overrightarrow{BE}=0 \\ \end{cases}$，$∴$$\begin{cases} y=0 \\ -2x+\dfrac{1}{2}y+\dfrac{a}{2}z=0 \\ \end{cases}$，

令$z=2$，解得$\begin{cases} x=\dfrac{a}{2} \\ y=0 \\ \end{cases}$，$∴$$\boldsymbol{n}=\left( \dfrac{a}{2},0,2 \right)$，

设平面$CPD$的法向量$\boldsymbol{m}=\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)$，又$\overrightarrow{CP}=(-2,-1,a)$，$\overrightarrow{C P}=(-2,-1, a), \overrightarrow{C D}=\overrightarrow{B A}=(-2,0,0)$ ，

则 $\begin{cases} \boldsymbol{m}\cdot \overrightarrow{CP}=0 \\ \boldsymbol{m}\cdot \overrightarrow{CD}=0 \\ \end{cases}$，$∴$$\begin{cases} -2{{x}_{0}}=0 \\ -2{{x}_{0}}-{{y}_{0}}+a{{z}_{0}}=0 \\ \end{cases}$，

令${{z}_{0}}=1$，解得 $\begin{cases} {{x}_{0}}=0 \\ {{y}_{0}}=a \\ \end{cases}$，$∴$$\boldsymbol{m}=(0,a,1)$，

设平面$BCE$与平面$CED$的夹角大小为$\theta $，

则$\cos \theta =|\cos \langle \boldsymbol{n},\boldsymbol{m}\rangle |=\left| \dfrac{\boldsymbol{n}\cdot \boldsymbol{m}}{|\boldsymbol{n}|\cdot |\boldsymbol{m}|} \right|=\dfrac{2}{\sqrt{\dfrac{{{a}^{2}}}{4}+4}\cdot \sqrt{{{a}^{2}}+1}}=\dfrac{4}{\sqrt{\left( {{a}^{2}}+16 \right)\left( {{a}^{2}}+1 \right)}}$$.$

$\because \sin \theta =\dfrac{\sqrt{21}}{5}$，

$\therefore \cos \theta =\dfrac{2}{5}$，

即$\dfrac{4}{\sqrt{\left( {{a}^{2}}+16 \right)\left( {{a}^{2}}+1 \right)}}=\dfrac{2}{5}$，$\dfrac{4}{\sqrt{\left(a^2+16\right)\left(a^2+1\right)}}=\dfrac{2}{5}, \quad\left(a^2-4\right)\left(a^2+21\right)=0$

解得$a=2$，即$PA=2$$.$