如图，在四棱锥${{P}-{ABCD}}$中，平面$P A B \perp$平面$ABCD$，$AD\perp CD$，$AD\text{//}BC$，$PA=AD=CD=1$，$BC=2$，$PB=\sqrt{3}$．$E$为${ {PD}}$的中点，点$F$在$PC$上，且$\dfrac{PF}{FC}=\dfrac{1}{2}$．

$(1)$求证：$PA\perp $平面$ABCD$；

$(2)$在棱$BP$上是否存在点$G$，使得点$G$到平面$AEF$的距离为$\dfrac{\sqrt{3}}{9}$，若存在求出点$G$的位置，不存在请说明理由．

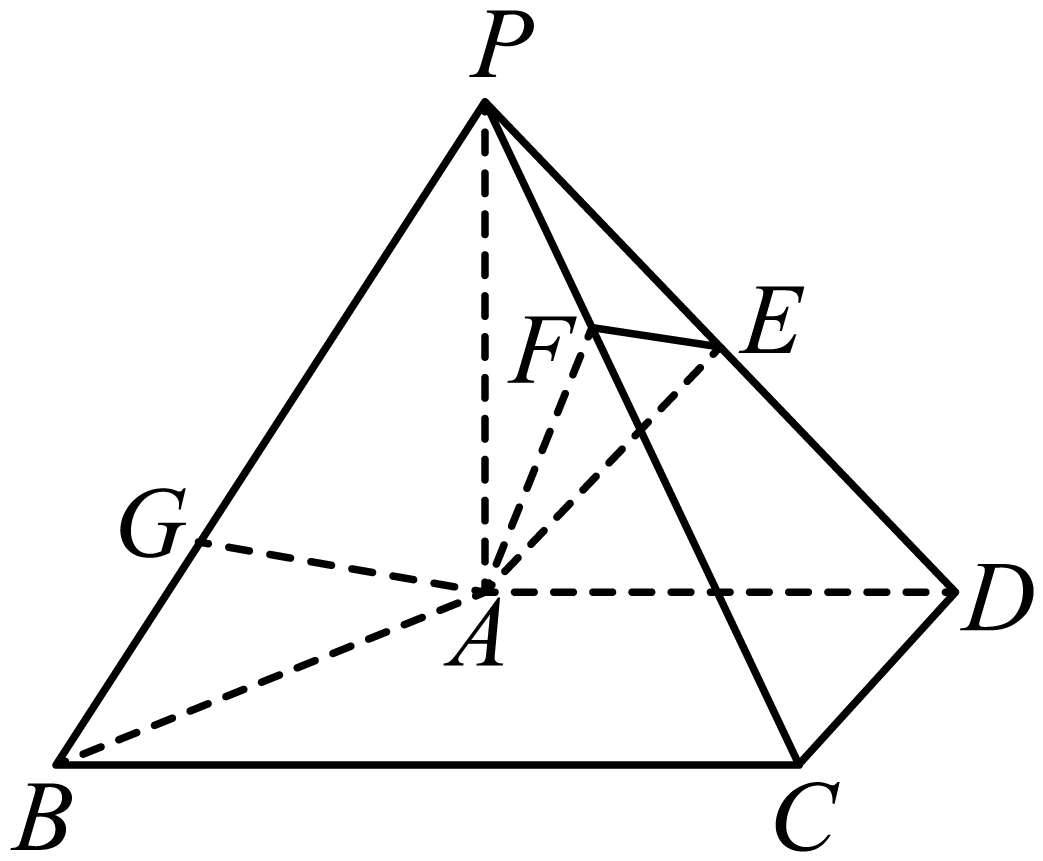
$(1)$证明见解析；$(2)$靠近$B$的三等分点

$(1)$取$BC$的中点$S$，连结$AS$，则四边形$ASCD$是正方形，

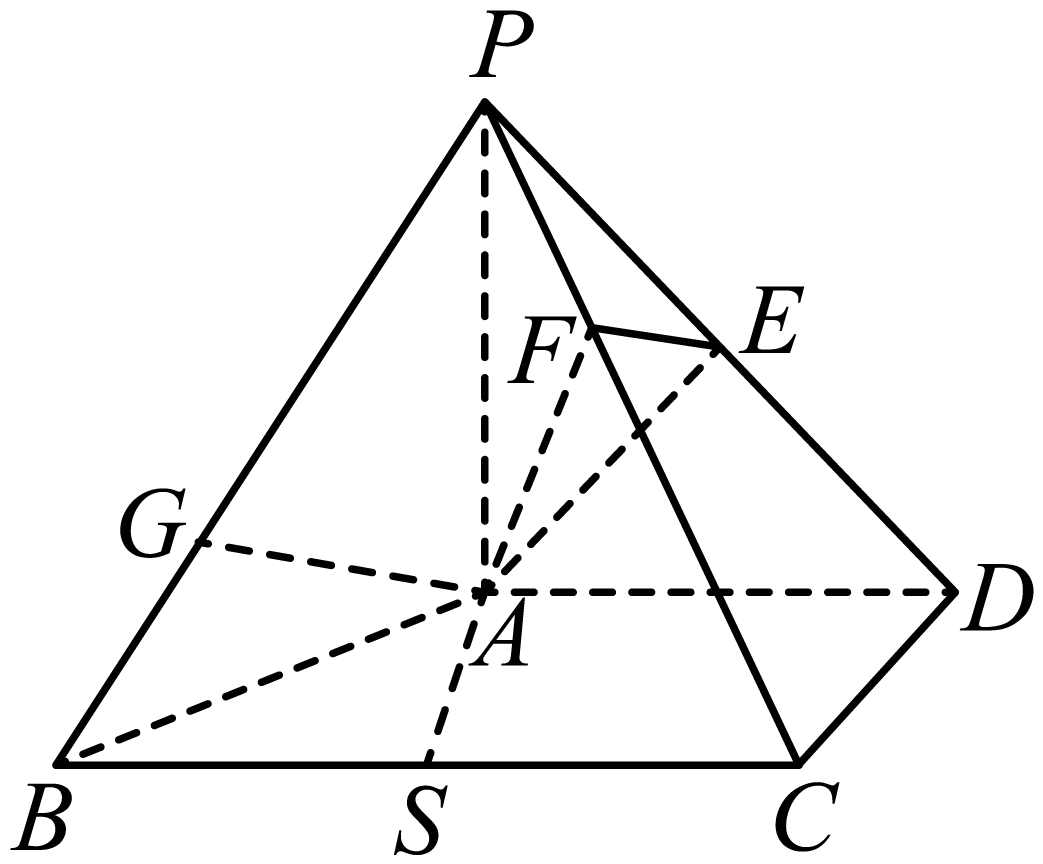
则$AS=BS=1$，$AS\perp BS$，

$\therefore AB=\sqrt{2}$，且$PA=1$，$PB=\sqrt{3}$

$\therefore P{{A}^{2}}+A{{B}^{2}}=P{{B}^{2}}$,

$\therefore PA\perp AB$，

$\because $ 平面$P A B \perp$平面$ABCD$，平面$P A B \cap$平面$A B C D=A B$，$PA$在面$PAB$内，

$\therefore PA\perp $平面$ABCD$；

$(2)$在$BC$上取点$M$，使$CM=\dfrac{3}{2}$，连结$PM$，在$PM$上取点$H$，使$\dfrac{MH}{MP}=\dfrac{1}{3}$，

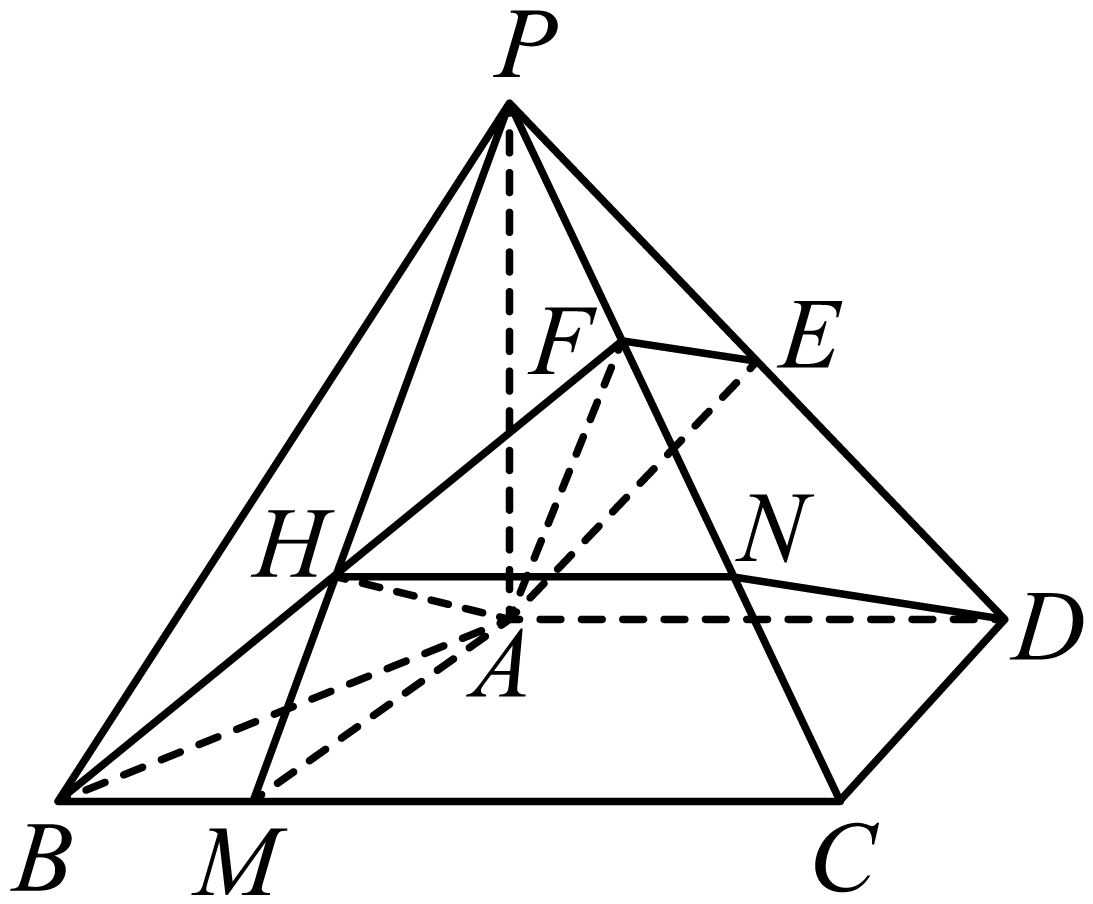
在$PC$上取点$N$，使$\dfrac{CN}{CP}=\dfrac{1}{3}$，连结$HN$，则$HN//BC$，且$\dfrac{HN}{MC}=\dfrac{2}{3}$，则$HN=1$，

即$HN//BC//AD$，且$HN=AD$，

则四边形$AHND$是平行四边形，

$\therefore AH//ND$，且$\dfrac{AF}{FN}=\dfrac{AE}{ED}$，即$EF//ND$，

则$EF//AH$，

$\therefore $ 四点$A$，$E$，$F$，$H$四点共面，连结$BH$，

$\overrightarrow{PH}=\dfrac{2}{3}\overrightarrow{PM}=\dfrac{2}{3}\left( \overrightarrow{PB}+\overrightarrow{BM} \right)=\dfrac{2}{3}\left( \overrightarrow{PB}+\dfrac{1}{4}\overrightarrow{BC} \right)$

$=\dfrac{2}{3}\left[ \overrightarrow{PB}+\dfrac{1}{4}\left( \overrightarrow{PC}-\overrightarrow{PB} \right) \right]=\dfrac{1}{2}\overrightarrow{PB}+\dfrac{1}{6}\overrightarrow{PC}$

$=\dfrac{1}{2}\overrightarrow{PB}+\dfrac{1}{2}\overrightarrow{PF}$，

$\because \dfrac{1}{2}+\dfrac{1}{2}=1$，

$\therefore $ 点$H$，$B$，$F$三点共线，

$\therefore A$，$E$，$F$，$H$，$B$五点共面，即$BP$与平面$AEF$交于点$B$，

由$(1)$可知，$PA\perp $平面$ABCD$，$CD\subset $平面$ABCD$，

$\therefore PA\perp CD$，且$AD\perp DC$，$PA\cap AD=A$，且$PA,AD\subset $平面$PAD$，

$\therefore CD\perp $平面$PAD$，$AE\subset $平面$PAD$，

$\therefore CD\perp AE$，

且$\triangle PAD$是等腰直角三角形，点$E$为${ {PD}}$的中点，

$\therefore AE\perp PD$，且$CD\cap PD=D$，$PD$，$CD\subset $平面$PCD$，

$\therefore AE\perp $平面$PCD$，

${{S}_{\triangle DEF}}=\dfrac{1}{6}{{S}_{\triangle PCD}}=\dfrac{1}{6}\times \dfrac{1}{2}\times PD\times CD=\dfrac{\sqrt{2}}{12}$，

$\therefore {{V}_{A-DEF}}=\dfrac{1}{3}\times {{S}_{\triangle DEF}}\times AE=\dfrac{1}{3}\times \dfrac{\sqrt{2}}{12}\times \dfrac{\sqrt{2}}{2}=\dfrac{1}{36}$，

$PE=\dfrac{\sqrt{2}}{2}$，$PF=\dfrac{1}{3}PC=\dfrac{\sqrt{3}}{3}$，$\cos \angle DPC=\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}$，

$\therefore E{{F}^{2}}=P{{E}^{2}}+P{{F}^{2}}-2PE\cdot PF\cdot \cos \angle DPC=\dfrac{1}{6}$，即$EF=\dfrac{\sqrt{6}}{6}$，

$\because AE\perp EF$，

$\therefore {{S}_{\triangle AEF}}=\dfrac{1}{2}\times AE\times EF=\dfrac{1}{2}\times \dfrac{\sqrt{2}}{2}\times \dfrac{\sqrt{6}}{6}=\dfrac{\sqrt{3}}{12}$，

设点$D$到平面$AEF$的距离为$h$，则${{V}_{D-AEF}}={{V}_{A-DEF}}$，

即$\dfrac{1}{3}\times \dfrac{\sqrt{3}}{12}\times h=\dfrac{1}{36}$，

$\therefore h=\dfrac{\sqrt{3}}{3}$，

$\because $ 点$E$是${ {PD}}$的中点，

$\therefore $ 点$P$到平面$AEF$的距离也是$\dfrac{\sqrt{3}}{3}$，

若点$G$到平面$AEF$的距离为$\dfrac{\sqrt{3}}{9}$，则$\dfrac{\dfrac{\sqrt{3}}{9}}{\dfrac{\sqrt{3}}{3}}=\dfrac{BG}{BP}=\dfrac{1}{3}$，

$\therefore $ 存在点$G$，使得点$G$到平面$AEF$的距离为$\dfrac{\sqrt{3}}{9}$，点$G$为靠近点$B$的三等分点．