如图，四边形$ABCD$中，$AD\perp AB$，$\angle ADC=120{}^\circ $，$AB=2\sqrt{3}$，$AD=1$，$CD=2$，

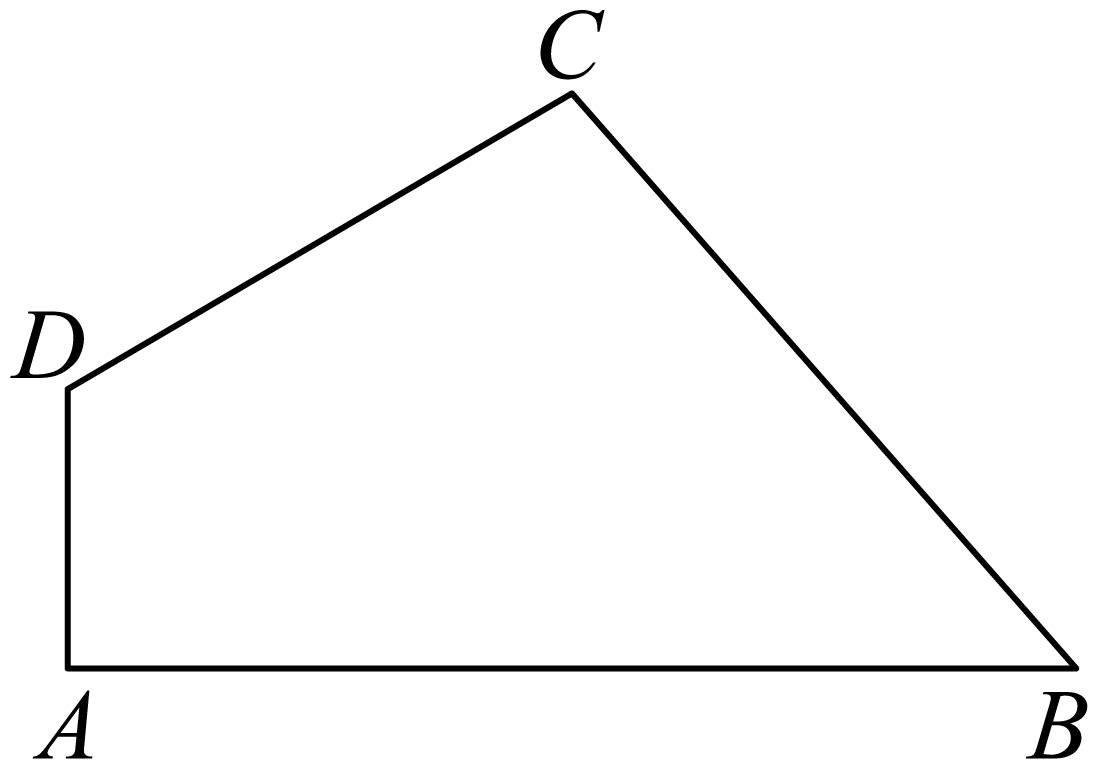
$(1)$求将四边形$ABCD$绕直线$AD$旋转一周所成几何体的体积；

$(2)$求将四边形$ABCD$绕直线$AB$旋转一周所成几何体的表面积．

$(1)$$13\\pi$

$(2)$$\\left( 2\\sqrt{7}+7 \\right)\\pi$

$(1)$作$CE\perp AD$，$CF\perp AB$，$E$，$F$为垂足，

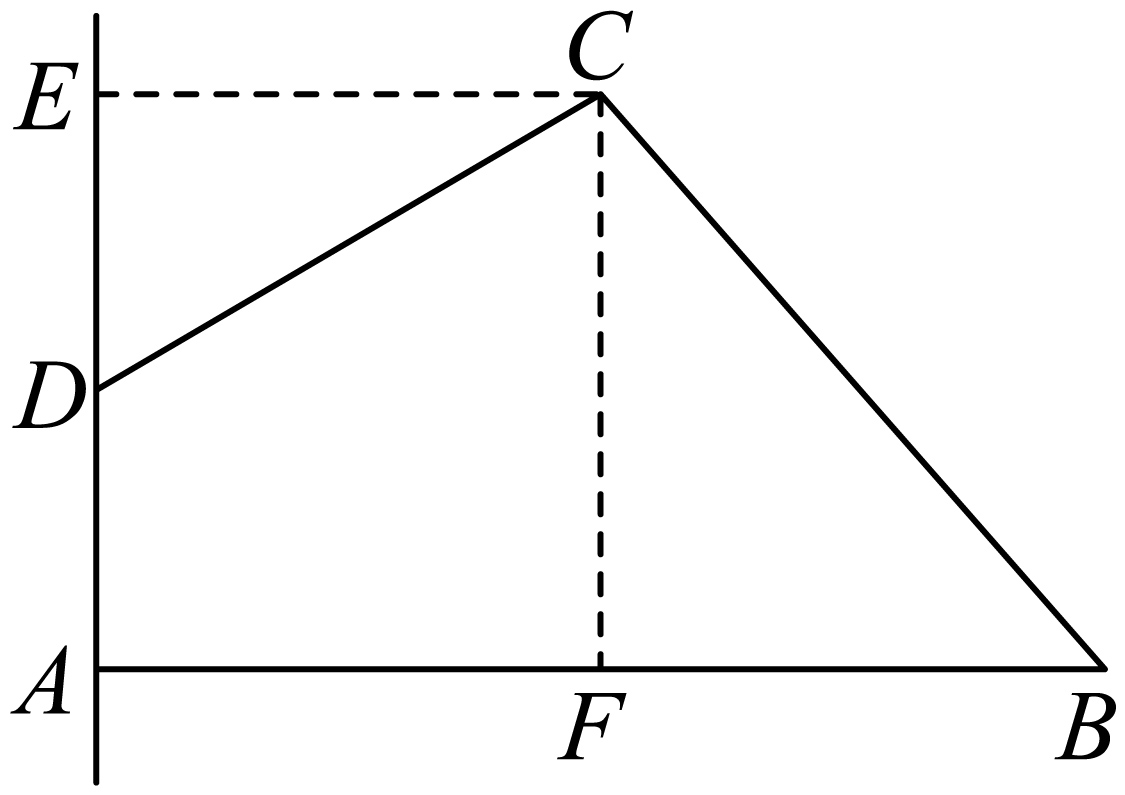
$\because \angle ADC=120{}^\circ $，

$\therefore \angle EDC=60{}^\circ $，

$\because CD=2$，

$\therefore DE=1$，$CE=\sqrt{3}$，

故$AF=CE=\sqrt{3}$，

又$AB=2\sqrt{3}$，$AD=1$，故$CF=AE=AD+DE=2$，

$BF=AB-AF=2\sqrt{3}-\sqrt{3}=\sqrt{3}$，

由勾股定理得$CB=\sqrt{C{{F}^{2}}+B{{F}^{2}}}=\sqrt{7}$，

由四边形$ABCE$绕直线$AD$旋转一周形成圆台，

且${V}_{圆台}=\dfrac{1}{3}\times 2\times \left( 3\pi+12\pi+6\pi \right)=14\pi$，

由三角形$CDE$绕直线$AD$旋转一周形成圆锥，

且${{V}_{圆锥}}=\dfrac{1}{3}\times 1\times 3\pi=\pi$

$\therefore $ 将四边形$ABCD$绕直线$AD$旋转一周所成几何体的体积为$14\pi-\pi=13\pi$；

$(2)$四边形$ABCD$绕直线$AB$旋转一周所成几何体的表面积分为三部分，

以$AD$为半径的圆的面积为$\pi$，

以$CD$为母线的圆台的侧面积$\pi l\left( r+{r}' \right)=2\pi\left( 1+2 \right)=6\pi$，

以$BC$为母线的圆锥的侧面积$\dfrac{1}{2}\times 2\times 2\pi\sqrt{7}=2\sqrt{7}\pi$，

$\therefore $ 该几何体的表面积为$\left( 2\sqrt{7}+7 \right)\pi$$.$