在三棱锥$P-ABC$中，$PA\perp $平面$ABC$，$AC\perp BC$，且$PA=AC=BC=2$，$E$为线段$PC$上的一个动点，则下列选项正确的是$(\qquad)$．

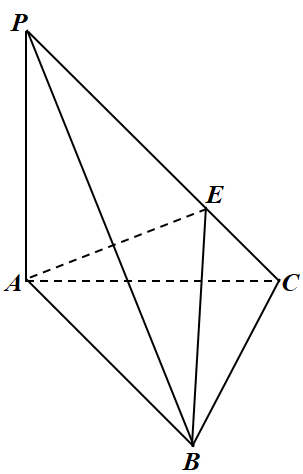
三棱锥$P-ABC$的表面积是$4+4\\sqrt{2}$

直线$PC$与直线$AB$所成的角为$60{}^\\circ $

$\\left| AE \\right|+\\left| BE \\right|$的最小值为$\\sqrt{2}+\\sqrt{6}$

三棱锥$P-ABC$外接球的表面积为$12\\pi $

$∵$$PA\perp $平面$ABC$，$AC\perp BC$

$∴$$PA\perp BCPA\perp ABPA\perp AC$，又$AC\perp BCPA\cap AC=C$

$∴$$BC\perp $平面$PAC$，$∴$$BC\perp PC$，又$PA=AC=BC=2$

$∴$三棱锥$P-ABC$的表面积是$\dfrac{1}{2}\times 2\times 2+\dfrac{1}{2}\times 2\times 2+\dfrac{1}{2}\times 2\sqrt{2}\times 2+\dfrac{1}{2}\times 2\sqrt{2}\times 2=4+4\sqrt{2}$，故选项$\rm A$正确；

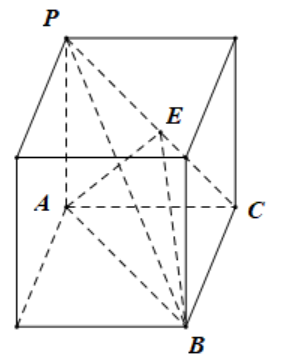
可以把三棱锥放入棱长为$2$正方体中如图，则易知直线$PC$与直线$AB$所成的角为$60{}^\circ $，

三棱锥$P-ABC$外接球即正方体的外接球，

$\therefore $ 外接球的表面积为$\pi \times ({{2}^{2}}+{{2}^{2}}+{{2}^{2}})=12\pi $，故选项$\rm B$、$\rm D$正确；

把$\triangle PCB$沿$PC$分翻折至平面$PAC$内，则$A{{B}_{1}}$的长即为$\left| AE \right|+\left| BE \right|$的最小值，

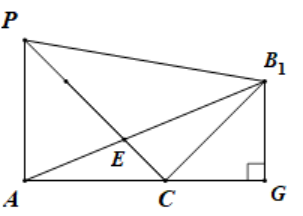
如图由题意可知${{B}_{1}}G=CG=\sqrt{2}$，则

$A{{B}_{1}}^{2}={{(\sqrt{2})}^{2}}+{{(2+\sqrt{2})}^{2}}=8+4\sqrt{2}$，

$∴$$A{{B}_{1}}=2\sqrt{2+\sqrt{2}}$，即$\left| AE \right|+\left| BE \right|$的最小值为$2\sqrt{2+\sqrt{2}}$，故选项$\rm C$错误$.$

故选：$\rm ABD$$.$