如图，圆台${{O}_{1}}{{O}_{2}}$，在轴截面$ABCD$中，$AB=AD=BC=\dfrac{1}{2}CD=2$，下面说法正确的是$(\qquad)$．

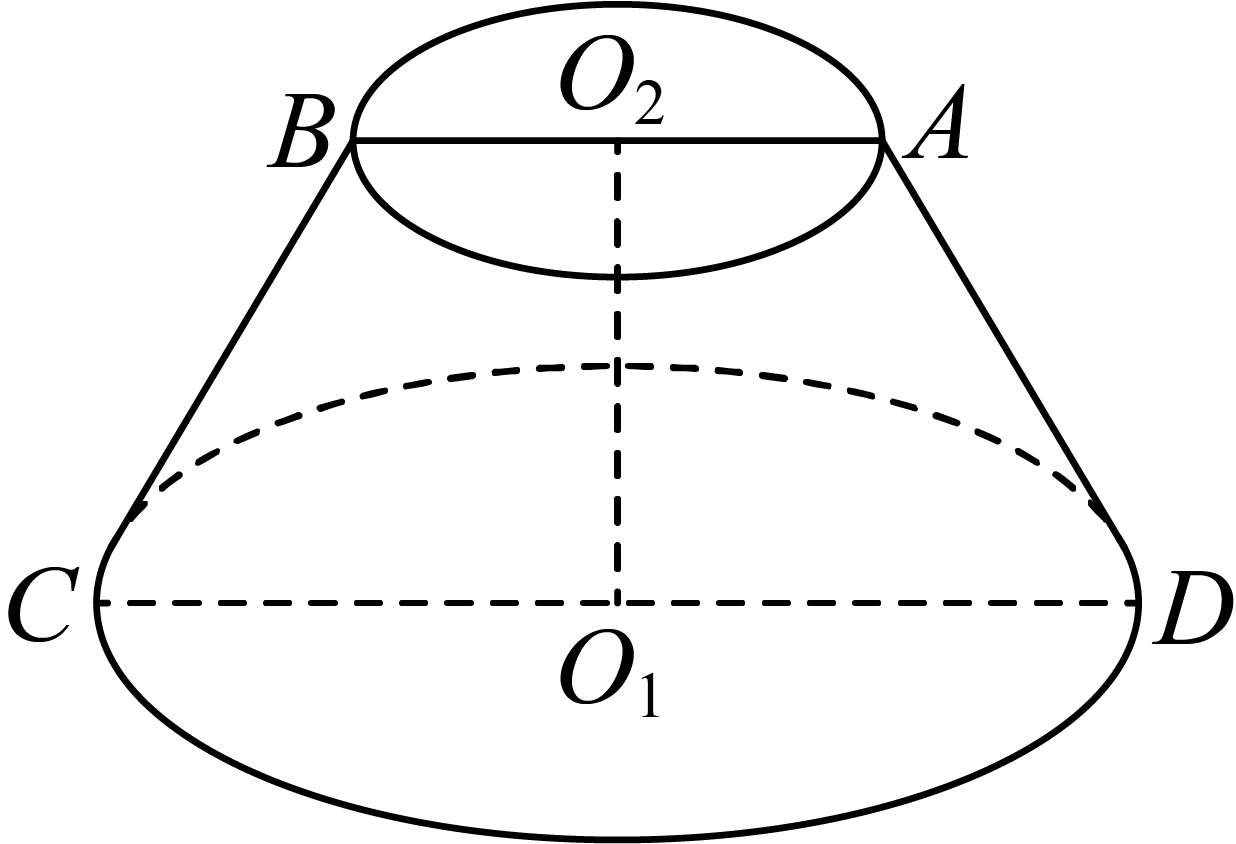
线段$AC=2\\sqrt{3}$

该圆台的表面积为$12\\pi$

该圆台的体积为$\\dfrac{7\\sqrt{3}}{3}\\pi$

沿着该圆台的表面，从点$C$到$AD$中点的最短距离为$5$

对于$\rm A$，如图：

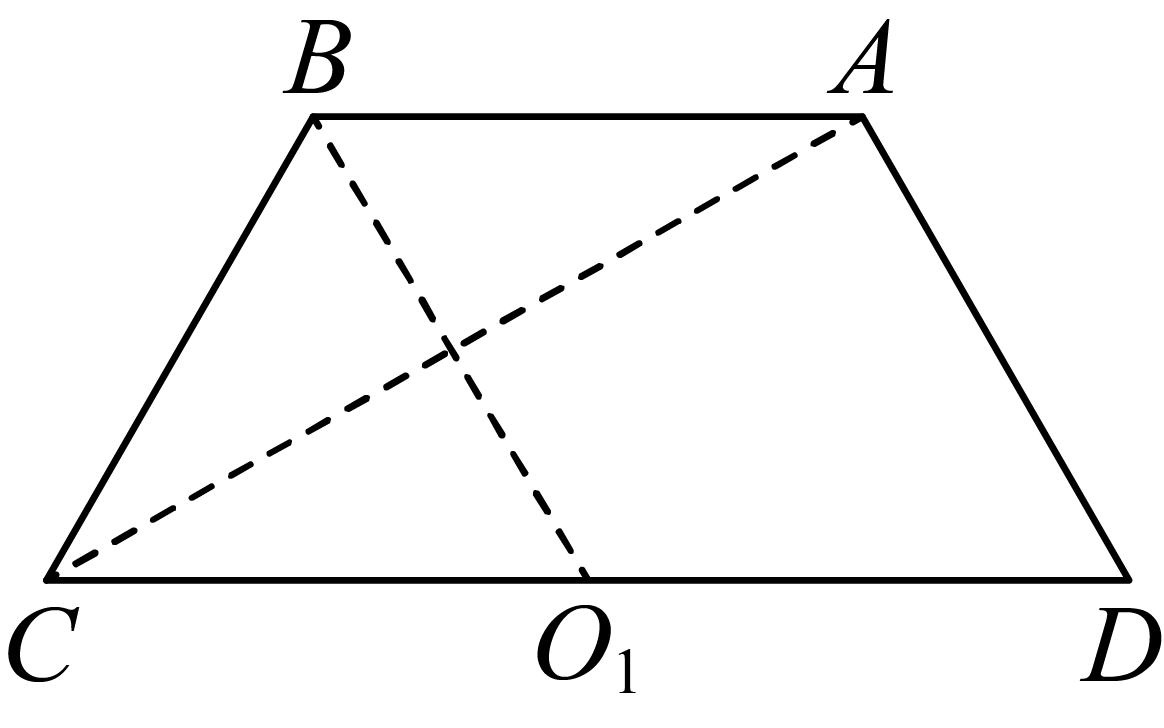
在截面$ABCD$中，$AB=AD=BC=\dfrac{1}{2}CD=2$，

$\because {{O}_{1}}$为$CD$的中点，

$\therefore C{{O}_{\text{1}}}={{O}_{\text{1}}}D=\text{2}$，

$\therefore AB={{O}_{\text{1}}}D$，且$AB\mathrm{}{{O}_{1}}D$，

$\therefore $ 四边形$AB{{O}_{1}}D$为平行四边形，

$\therefore B{{O}_{\text{1}}}=AD=\text{2}$，

$\therefore \triangle BC{{O}_{1}}$为等边三角形，

$\therefore \angle BC{{O}_{\text{1}}}=\text{6}0{}^\circ $，$\angle CBA=\text{12}0{}^\circ $，

在等腰$\triangle ABC$中，$AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}-2AB\cdot BC\cos B}=\sqrt{3}AB=2\sqrt{3}$，正确；

对于$\rm B$，设圆台上底面半径为${{r}_{\text{1}}}$，下底面半径为${{r}_{\text{2}}}$，母线为$l$，则${{r}_{\text{1}}}=\text{1}$，${{r}_{\text{2}}}=\text{2}$，$l=\text{2}$，

则圆台的表面积$S={{S}_{上}}+{{S}_{下}}+{{S}_{侧}}=\pi r_{1}^{2}+\left( \pi{{r}_{1}}+\pi{{r}_{2}} \right)l+\pi r_{2}^{2}=\pi+6\pi+4\pi=11\pi$，错误；

对于$\rm C$，由$B$知圆台的高为$h=\sqrt{{{2}^{2}}-{{\left( 2-1 \right)}^{2}}}=\sqrt{3}$，

$\therefore $ 圆台的体积$V=\dfrac{1}{3}\times \left( {{1}^{2}}+\sqrt{{{1}^{2}}\times {{2}^{2}}}+{{2}^{2}} \right)\times \sqrt{3}\pi=\dfrac{\text{7}\sqrt{\text{3}}}{3}\pi$，正确；

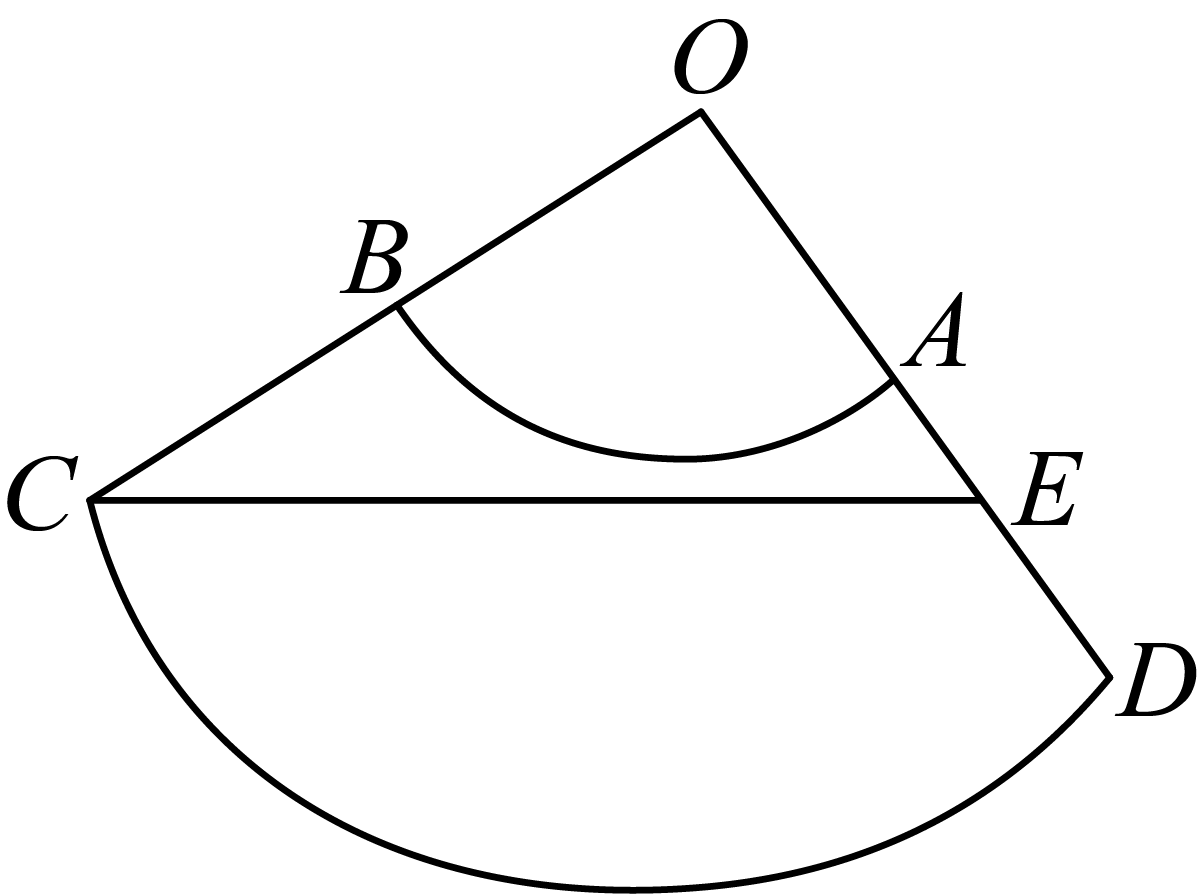
对于$\rm D$，将圆台一半侧面展开，如图中$ABCD$，且$E$为$AD$的中点，

而圆台对应的圆锥体侧面展开为扇形$COD$，且$OC=\text{4}$，$\angle COD=\dfrac{2\pi}{4}=\dfrac{\pi}{2}$，

$\therefore $ 在$\text{Rt}\triangle COE$中，$CE=\sqrt{{{4}^{2}}+{{3}^{2}}}=5$，即$C$到$AD$中点的最短距离为$5$，正确$.$

故选：$\rm ACD$