如图，已知正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$，点$E$、$F$、$G$分别为棱$BC$、$C{{C}_{1}}$、$CD$的中点，下列结论正确的有$(\qquad)$．

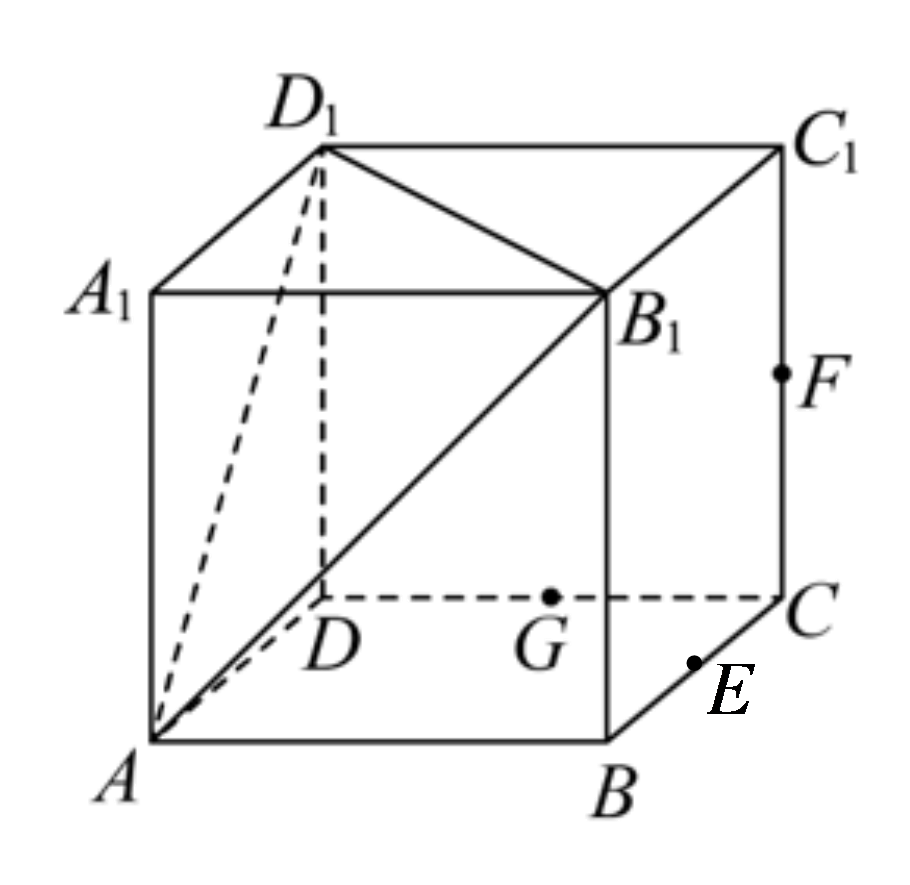
$AE$与${{D}_{1}}F$共面

平面$A{{B}_{1}}{{D}_{1}}\\text{//}$平面$GFE$

$AE\\perp EF$

$BF//$平面$A{{B}_{1}}{{D}_{1}}$

如下图所示：

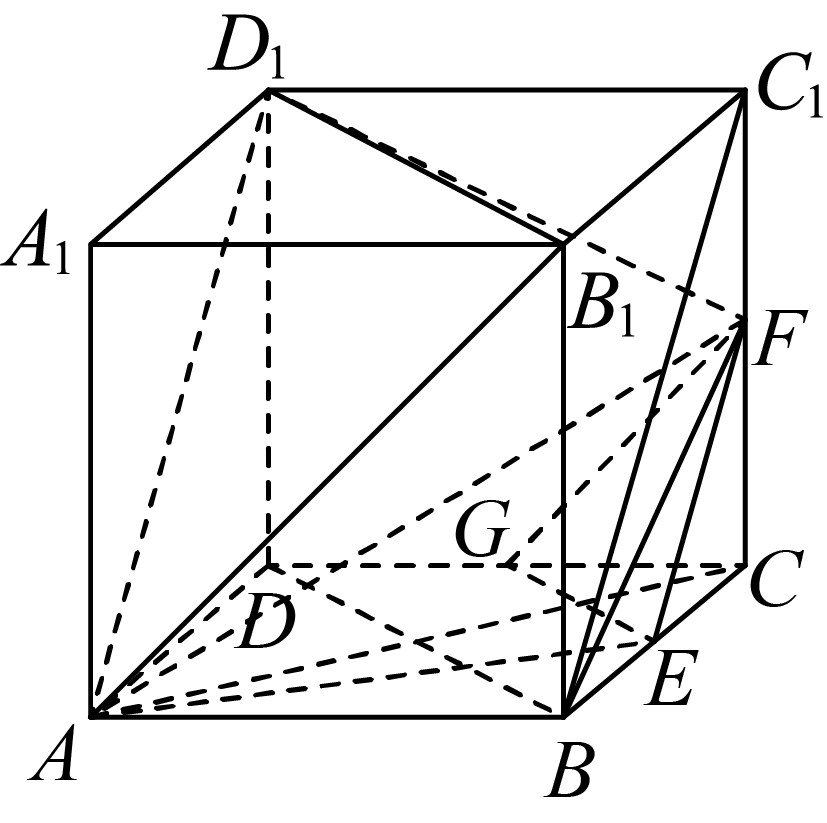
对于$\rm A$选项，连接$B{{C}_{1}}$，

在正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$中，$AB\text{//}{{C}_{1}}{{D}_{1}}$且$AB={{C}_{1}}{{D}_{1}}$，

$\therefore $ 四边形$A B C_1 D_1$为平行四边形，则$B{{C}_{1}}\text{//}A{{D}_{1}}$，

$\because E$、$F$分别为$BC$、$C{{C}_{1}}$的中点，则$EF\text{//}B{{C}_{1}}$，故$EF\text{//}A{{D}_{1}}$，

$\therefore $ $AE$与${{D}_{1}}F$共面，$\rm A$对；

对于$\rm B$选项，

$\because B{{B}_{1}}\text{//}D{{D}_{1}}$且$B{{B}_{1}}=D{{D}_{1}}$，

$\therefore $ ，四边形$B{{B}_{1}}{{D}_{1}}D$为平行四边形，

则$BD\text{//}{{B}_{1}}{{D}_{1}}$，

又$\because E$、$G$分别为$BC$、$CD$的中点，则$EG\text{//}BD$，

$\therefore $ $EG\text{//}{{B}_{1}}{{D}_{1}}$，

$\because EG\not\subset $平面$A{{B}_{1}}{{D}_{1}}$，$B_{1} D_{1} \subset$平面$A{{B}_{1}}{{D}_{1}}$，

$\therefore $ ，$EG\text{//}$平面$A{{B}_{1}}{{D}_{1}}$，

同理可证$EF\text{//}$平面$A{{B}_{1}}{{D}_{1}}$，

$\because EF\cap EG=E$，$EF$、$EG\subset $平面$EFG$，

$\therefore $ 平面$EFG\text{//}$平面$A{{B}_{1}}{{D}_{1}}$，$\rm B$对；

对于$\rm C$选项，不妨设$ABCD$的棱长为$2$，则$AE=\sqrt{A{{B}^{2}}+B{{E}^{2}}}=\sqrt{4+1}=\sqrt{5}$，

$EF=\sqrt{C{{E}^{2}}+C{{F}^{2}}}=\sqrt{1+1}=\sqrt{2}$，$AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{4+4}=2\sqrt{2}$，

$\because C{{C}_{1}}\perp $平面$ABCD$，$AC\subset $平面$ABCD$，则$C{{C}_{1}}\perp AC$，

$\therefore $ $AF=\sqrt{A{{C}^{2}}+C{{F}^{2}}}=\sqrt{8+1}=3$，

$\therefore $ $A{{E}^{2}}+E{{F}^{2}}\ne A{{F}^{2}}$，故$AE$、$EF$不垂直，$\rm C$错；

对于$\rm D$选项，假设$BF\text{//}$平面$A{{B}_{1}}{{D}_{1}}$，

又$\because EF\text{//}$平面$A{{B}_{1}}{{D}_{1}}$，$EF\cap BF=F$，$EF$、$BF\subset $平面$B{{B}_{1}}{{C}_{1}}C$，

$\therefore $ 平面$B{{B}_{1}}{{C}_{1}}C\text{//}$平面$A{{B}_{1}}{{D}_{1}}$，

事实上，平面$B{{B}_{1}}{{C}_{1}}C$与平面$A{{B}_{1}}{{D}_{1}}$不平行，假设不成立，$\rm D$错$.$

故选：$\rm AB$