如图，在等腰梯形$ABCD$中，$AB\mathrm{}CD$，$AD=DC=3$，$\angle BCD=120{}^\circ $，$DE\perp $平面$ABCD$，$BF\perp $平面$ABCD$，$BF=DE=3$，点$P$在线段$EF$上运动$.$

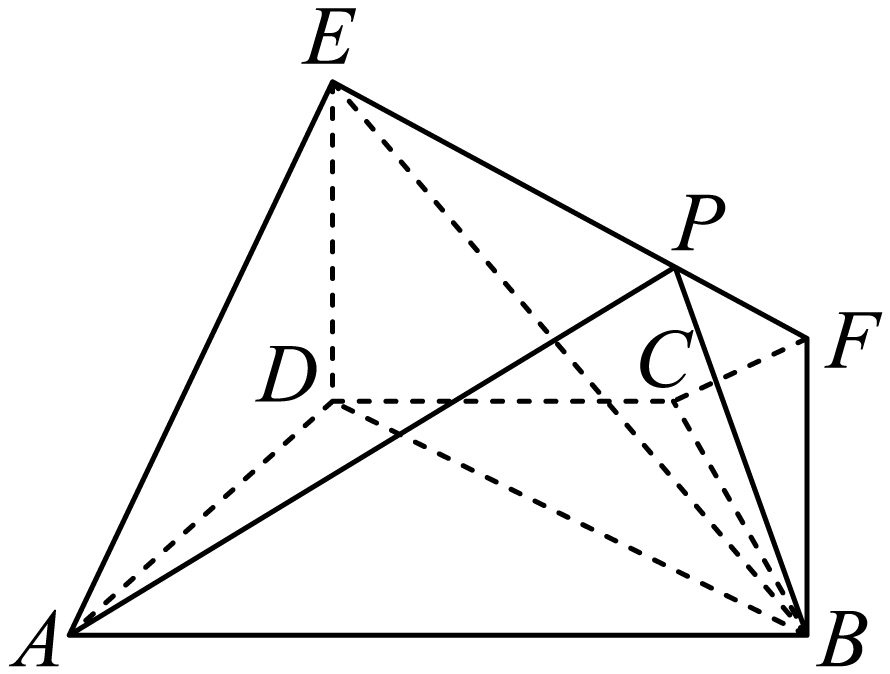
$(1)$求证：$AD\perp BP$；

$(2)$是否存在点$P$，使得$PB\mathrm{}$平面$ACE$？若存在，试求点$P$的位置；若不存在，请说明理由$.$

$(1)$证明见解析；

$(2)$存在，$EP=2\\sqrt{3}$

$(1)$证明：在等腰梯形$ABCD$中，

$∵$$AB\mathrm{}CD$，$AD=DC=CB=\text{3}$，$\angle BCD=\text{12}0{}^\circ $，

$∴$$AB=6$，

$∴$$B{{D}^{\text{2}}}=A{{B}^{\text{2}}}+A{{D}^{\text{2}}}-\text{2}AB\ \cdot \ AD\ \cdot \ \text{cos6}0{}^\circ =\text{27}$，

$∴$$A{{B}^{\text{2}}}=A{{D}^{\text{2}}}+B{{D}^{\text{2}}}$，

$∴$$AD\perp BD$$.$

$∵$$DE\perp $平面$ABCD$，$A D \subset$平面$ABCD$，

$∴$$DE\perp AD$$.$

又$∵$$BD\cap DE=D$，$BD$，$DE\subset $平面$BFED$，

$∴$$A D \perp$平面$BFED$$.$

$∵$$BP\subset $平面$BFED$，

$∴$$AD\perp BP$$.$

$(2)$在线段$EF$上存在$P$且$EP=2\sqrt{3}$,使得$PB\mathrm{}$平面$ACE$$.$

证明如下：由已知可得四边形$BFED$为矩形，连接$AC$交$BD$于$O$，连接$OE$，

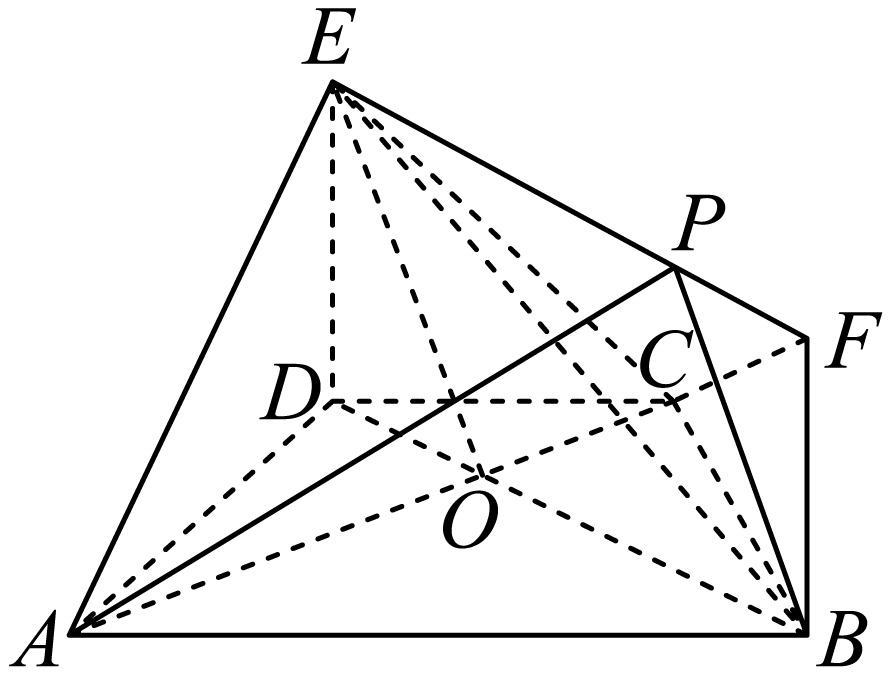
由$(1)$知在$\text{Rt}\triangle ABD$中，$BD=3\sqrt{3}$，$AD=3$，$AB=6$$.$

$∵$$AB\mathrm{}CD$，

$∴$$\dfrac{DC}{AB}=\dfrac{DO}{OB}=\dfrac{1}{2}$，

$∴$$OB=2\sqrt{3}$$.$

当$EP=2\sqrt{3}$时，$EP\mathrm{}OB$且$EP=OB$，

则四边形$OBPE$为平行四边形，

则$BP\mathsf{\parallel }OE$$.$

又$BP\not\subset $平面$AEC$，$OE\subset $平面$AEC$，

$\therefore BP\mathrm{}$平面$AEC$$.$

综上可知，在线段$EF$上存在$P$，使得$PB\mathrm{}$平面$ACE$，且$EP=2\sqrt{3}$$.$