已知函数$f\left( x \right)=\dfrac{{{x}^{2}}+x-1}{{{\text{e}}^{x}}}$，则$(\qquad)$．

函数$f\\left( x \\right)$有且只有两个零点

函数$f\\left( x \\right)$在$\\left( -1,2 \\right)$上为增函数

函数$f\\left( x \\right)$的最大值为$5{{\\text{e}}^{-2}}$

若方程$f\\left( x \\right)=a$有三个实根，则$a\\in \\left( 0,5{{\\text{e}}^{-2}} \\right)$

令$f\left( x \right)=0$，则${{x}^{2}}+x-1=0$，

$∴$${{x}_{1}}=\dfrac{-1-\sqrt{5}}{2}$，${{x}_{2}}=\dfrac{-1+\sqrt{5}}{2}$，

$\therefore $ 函数$f\left( x \right)$有且只有两个零点，故$\rm A$正确；

由已知${f}'\left( x \right)=\dfrac{-{{x}^{2}}+x+2}{{{\text{e}}^{x}}}$，

令${f}'\left( x \right)\gt 0$，得$-1\lt x\lt 2$，

令${f}'\left( x \right)\lt 0$，得$x\lt -1$或$x\gt 2$，

$∴$$f\left( x \right)$在$\left( -1,2 \right)$上为增函数，在$\left( -\infty ,-1 \right)$，$\left( 2,+\infty \right)$上为减函数，故$\rm B$正确；

$f{{\left( x \right)}_{}}=f\left( 2 \right)=5{{\text{e}}^{-2}}$，$f{{\left( x \right)}_{}}=f\left( -1 \right)=-\text{e}$，

解不等式$f\left( x \right)\gt 0$，得$x\lt {{x}_{1}}$或$x\gt {{x}_{2}}$，

解不等式$f\left( x \right)\lt 0$，得${{x}_{1}}\lt x\lt {{x}_{2}}$，

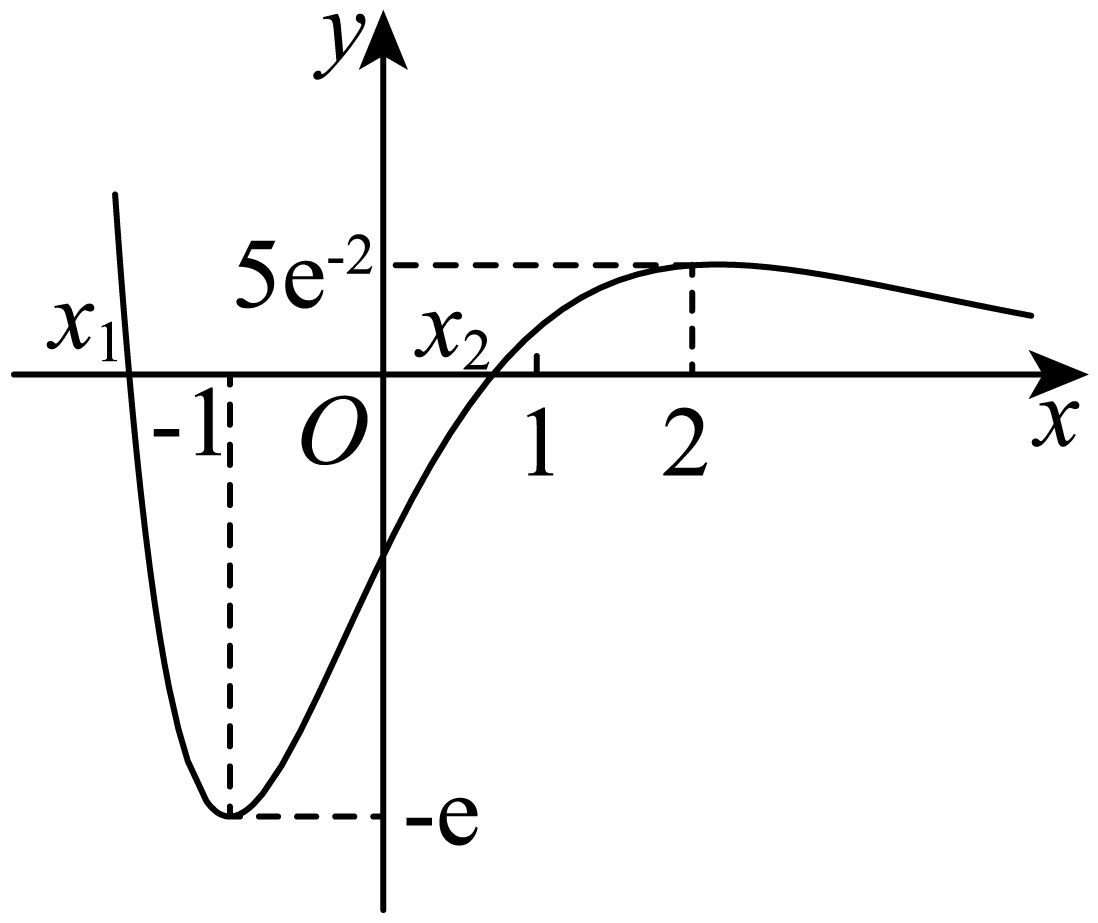
当$x\rightarrow +\infty$时，$f\left( x \right)\to 0$，当$x\to -\infty $时，$f\left( x \right)\to +\infty $，

作出$f\left( x \right)$的图象，由图象得，$f\left( x \right)$无最大值，故$\rm C$错误；

方程$f\left( x \right)=a$有三个实根，即$y=f\left( x \right)$与$y=a$的图象有三个不同的交点，

$∴$$0\lt a\lt 5{{\text{e}}^{-2}}$，故$\rm D$正确，

故选：$\rm ABD$．