已知定义在$\left( -\infty ,-\dfrac{1}{2} \right)\cup \left( \dfrac{1}{2},+\infty \right)$上的函数$f\left( x \right)$同时满足下列四个条件：

①$f\left( \dfrac{5}{2} \right)=-1$；

②对任意$\left| x \right|\gt \dfrac{1}{2}$，恒有$f\left( -x \right)+f\left( x \right)=0$；

③对任意$x\gt \dfrac{3}{2}$，恒有$f\left( x \right)\lt 0$；

④对任意$a,b\gt 0$，恒有$f\left( a+\dfrac{1}{2} \right)+f\left( b+\dfrac{1}{2} \right)=f\left( ab+\dfrac{1}{2} \right)$．

$(1)$求$f\left( -\dfrac{3}{2} \right)$的值；

$(2)$判断$f\left( x \right)$在$\left( \dfrac{1}{2},+\infty \right)$上的单调性，并用定义法证明；

$(3)$若对任意$t\in \left[ -1,1 \right]$，恒有$f\left( -{{t}^{2}}+\left( 1-2k \right)t+3k \right)\leqslant 2$，求实数$k$的取值范围．

$(1)$$0$；

$(2)$$f\\left( x \\right)$在$\\left( \\dfrac{1}{2},+\\infty \\right)$上单调递减，证明见解析；

$(3)$$\\left[ \\dfrac{3}{4},+\\infty \\right)$

$(1)$在$f\left( a+\dfrac{1}{2} \right)+f\left( b+\dfrac{1}{2} \right)=f\left( ab+\dfrac{1}{2} \right)$中令$a=b=1\Rightarrow 2f\left( \dfrac{3}{2} \right)=f\left( \dfrac{3}{2} \right)\Rightarrow f\left( \dfrac{3}{2} \right)=0$；

（或令$a=2$，$b=1\Rightarrow f\left( \dfrac{5}{2} \right)+f\left( \dfrac{3}{2} \right)=f\left( \dfrac{5}{2} \right)\Rightarrow f\left( \dfrac{3}{2} \right)=0$$)$．

而$f\left( -x \right)+f\left( x \right)=0\Rightarrow f\left( -\dfrac{3}{2} \right)+f\left( \dfrac{3}{2} \right)=0\Rightarrow f\left( -\dfrac{3}{2} \right)=0$；

$(2)$$f\left( x \right)$在$\left( \dfrac{1}{2},+\infty \right)$上单调递减．

下证明：

由④知：对任意$a$，$b\gt 0$，恒有$f\left( ab+\dfrac{1}{2} \right)-f\left( b+\dfrac{1}{2} \right)=f\left( a+\dfrac{1}{2} \right)$．

证一：任取${{x}_{2}}\gt {{x}_{1}}\gt \dfrac{1}{2}$，

于是$f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)=f\left( \dfrac{{{x}_{2}}-\dfrac{1}{2}}{{{x}_{1}}-\dfrac{1}{2}}\cdot \left( {{x}_{1}}-\dfrac{1}{2} \right)+\dfrac{1}{2} \right)-f\left( \left( {{x}_{1}}-\dfrac{1}{2} \right)+\dfrac{1}{2} \right)=f\left( \dfrac{{{x}_{2}}-\dfrac{1}{2}}{{{x}_{1}}-\dfrac{1}{2}}+\dfrac{1}{2} \right)$

$\because {{x}_{2}}\gt {{x}_{1}}\gt \dfrac{1}{2}$，

$\therefore {{x}_{2}}-\dfrac{1}{2}\gt {{x}_{1}}-\dfrac{1}{2}\gt 0$

$\Rightarrow \dfrac{{{x}_{2}}-\dfrac{1}{2}}{{{x}_{1}}-\dfrac{1}{2}}\gt 1\Rightarrow \dfrac{{{x}_{2}}-\dfrac{1}{2}}{{{x}_{1}}-\dfrac{1}{2}}+\dfrac{1}{2}\gt \dfrac{3}{2}$，

而对任意$x\gt \dfrac{3}{2}$时恒有$f\left( x \right)\lt 0$，故$f\left( \dfrac{{{x}_{2}}-\dfrac{1}{2}}{{{x}_{1}}-\dfrac{1}{2}}+\dfrac{1}{2} \right)\lt 0$，

即$f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)\lt 0$，

$\therefore f\left( x \right)$在$\left( \dfrac{1}{2},+\infty \right)$上单调递减，证毕；

证二：任取${{x}_{2}}\gt {{x}_{1}}\gt \dfrac{1}{2}$，设${{x}_{2}}=mn+\dfrac{1}{2}$，${{x}_{1}}=n+\dfrac{1}{2}$，$m\gt 1$，$n\gt 0$

$f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)=f\left( mn+\dfrac{1}{2} \right)-f\left( n+\dfrac{1}{2} \right)=f\left( m+\dfrac{1}{2} \right)$，

$\because m\gt 1$，$m+\dfrac{1}{2}\gt \dfrac{3}{2}$，

$\therefore f\left( m+\dfrac{1}{2} \right)\lt 0$，即$f\left( {{x}_{2}} \right)\lt f\left( {{x}_{1}} \right)$，

也即$f\left( x \right)$在$\left( \dfrac{1}{2},+\infty \right)$单调递减,证毕；

$(3)$在$f\left( a+\dfrac{1}{2} \right)+f\left( b+\dfrac{1}{2} \right)=f\left( ab+\dfrac{1}{2} \right)$中：

令$a=b=2\Rightarrow f\left( \dfrac{5}{2} \right)+f\left( \dfrac{5}{2} \right)=f\left( \dfrac{9}{2} \right)\Rightarrow f\left( \dfrac{9}{2} \right)=-2$，

而$f\left( -x \right)+f\left( x \right)=0$，于是$f\left( -\dfrac{9}{2} \right)=2$，

令$a=\dfrac{1}{4}$，$b=4\Rightarrow f\left( \dfrac{3}{4} \right)+f\left( \dfrac{9}{2} \right)=f\left( \dfrac{3}{2} \right)=0\Rightarrow f\left( \dfrac{3}{4} \right)=-f\left( \dfrac{9}{2} \right)=2$，

由$(2)$知$f\left( x \right)$在$\left( \dfrac{1}{2},+\infty \right)$上单调递减，

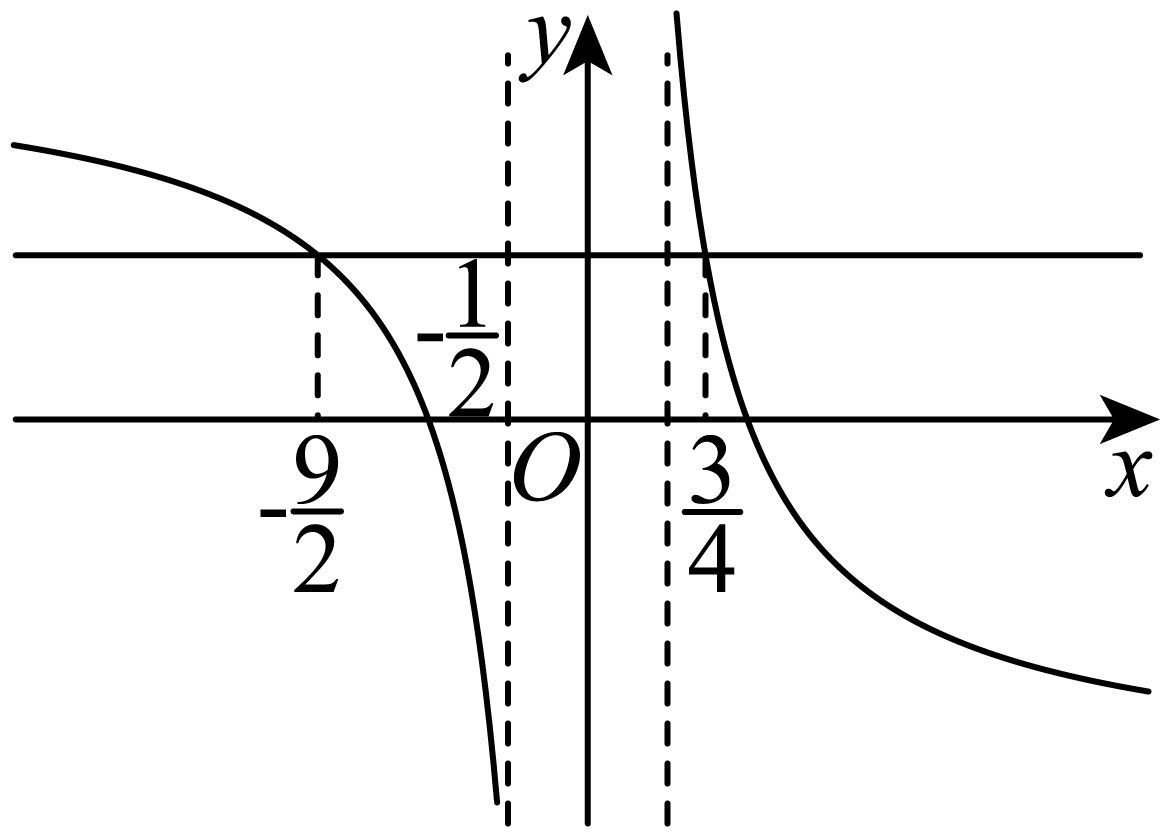
又$f\left( -x \right)+f\left( x \right)=0$，可得$f\left( x \right)$在$\left( -\infty ,-\dfrac{1}{2} \right)$上也单调递减，如图，

可知不等式$f\left( -{{t}^{2}}+\left( 1-2k \right)t+3k \right)\leqslant 2$等价于：

对任意$t\in \left[ -1,1 \right]$，不等式

$-{{t}^{2}}+\left( 1-2k \right)t+3k\geqslant \dfrac{3}{4}$……①

或者$-\dfrac{9}{2}\leqslant -{{t}^{2}}+\left( 1-2k \right)t+3k\lt -\dfrac{1}{2}$恒成立，……②

法一：令$g\left( t \right)=-{{t}^{2}}+\left( 1-2k \right)t+3k$，$t\in \left[ -1,1 \right]$，

$\because g\left( t \right)$开口向下，由$g\left( t \right)$图像可知：

不等式①$\Leftrightarrow \left\{ \begin{array}{l} { g\left( -1 \right)\geqslant \dfrac{3}{4} }\\{g\left( 1 \right)\geqslant \dfrac{3}{4}} \end{array}\right.\Rightarrow \left\{ \begin{array}{l} {k\geqslant \dfrac{11}{20}}\\{k\geqslant \dfrac{3}{4}} \end{array}\right.\Rightarrow k\geqslant \dfrac{3}{4}$；

对于②，当$t=\pm 1$时，由$\left\{ \begin{array}{l} {-\dfrac{9}{2}\leqslant g\left( -1 \right)\lt -\dfrac{1}{2}}\\{-\dfrac{9}{2}\leqslant g\left( 1 \right)\lt -\dfrac{1}{2}} \end{array}\right. \Rightarrow \left\{ \begin{array}{l} {-\dfrac{1}{2}\leqslant k\lt \dfrac{3}{10}}\\{-\dfrac{9}{2}\leqslant k\lt -\dfrac{1}{2}} \end{array}\right.\Rightarrow k\in \varnothing $，

即一定不存在$k$满足②．

综上取并，得$k\in \left[ \dfrac{3}{4},+\infty \right)$．

法二：

令$g\left( t \right)=-{{t}^{2}}+\left( 1-2k \right)t+3k$，$t\in \left[ -1,1 \right]$，$g\left( t \right)$开口向下，对称轴为$t=\dfrac{1}{2}-k$，

且$g\left( -1 \right)=5k-2$，$g\left( 1 \right)=k$，$g\left( \dfrac{1}{2}-k \right)={{k}^{2}}+2k+\dfrac{1}{4}$，

${{1}^{^\circ }}$当$\dfrac{1}{2}-k\lt -1$即$k\gt \dfrac{3}{2}$时，问题等价于$\begin{cases} k\gt \dfrac{3}{2} \\ g\left( 1 \right)\geqslant \dfrac{3}{4} \\ \end{cases}$或$\begin{cases} k\gt \dfrac{3}{2} \\ g\left( -1 \right)\lt -\dfrac{1}{2} \\ g\left( 1 \right)\geqslant -\dfrac{9}{2} \\ \end{cases}$，解得$k\gt \dfrac{3}{2}$；

${{2}^{^\circ }}$当$-1\leqslant \dfrac{1}{2}-k\leqslant 0$即$\dfrac{1}{2}\leqslant k\leqslant \dfrac{3}{2}$时，等价于$\begin{cases} \dfrac{1}{2}\leqslant k\leqslant \dfrac{3}{2} \\ g\left( 1 \right)\geqslant \dfrac{3}{4} \\ \end{cases}$或$\begin{cases} \dfrac{1}{2}\leqslant k\leqslant \dfrac{3}{2} \\ g\left( \dfrac{1}{2}-k \right)\lt -\dfrac{1}{2} \\ g\left( 1 \right)\geqslant -\dfrac{9}{2} \\ \end{cases} \Rightarrow k\in \left[ \dfrac{3}{4},\dfrac{3}{2} \right]$；

${{3}^{^\circ }}$当$0\lt \dfrac{1}{2}-k\leqslant 1$即$-\dfrac{1}{2}\leqslant k\lt \dfrac{1}{2}$时，问题等价于$\begin{cases} -\dfrac{1}{2}\leqslant k\lt \dfrac{1}{2} \\ g\left( -1 \right)\geqslant \dfrac{3}{4} \\ \end{cases}$或$\begin{cases} -\dfrac{1}{2}\leqslant k\lt \dfrac{1}{2} \\ g\left( \dfrac{1}{2}-k \right)\lt -\dfrac{1}{2} \\ g\left( -1 \right)\geqslant -\dfrac{9}{2} \\ \end{cases}$，

解得$k\in \varnothing $；

${{4}^{^\circ }}$当$\dfrac{1}{2}-k\gt 1$即$k\lt -\dfrac{1}{2}$时，问题等价于$\begin{cases} k\lt -\dfrac{1}{2} \\ g\left( -1 \right)\geqslant \dfrac{3}{4} \\ \end{cases}$或$\begin{cases} k\lt -\dfrac{1}{2} \\ g\left( 1 \right)\lt -\dfrac{1}{2} \\ g\left( -1 \right)\geqslant -\dfrac{9}{2} \\ \end{cases}$，

解得$k\in \varnothing $；

综上，$k\in \left[ \dfrac{3}{4},+\infty \right)$．