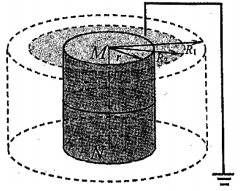
求电子到达金属圆柱网面速度大小${{v}_{1}}$；

电子到达金属圆柱网面速度大小为$\\sqrt{\\dfrac{2eU}{m}}$；

根据动能定理$eU=\dfrac{1}{2}mv_{1}^{2}$得：电子到达金属圆柱网面速度大小${{v}_{1}}=\sqrt{\dfrac{2eU}{m}}$；

要求没有电子能飞出半径${{R}_{1}}$的圆柱侧面，求磁感应强度的最小值$B$；

磁感应强度的最小值为$\\dfrac{1}{3r}\\sqrt{\\dfrac{6mU}{e}}$；

根据题意，没有电子能飞出半径${{R}_{1}}$的圆柱侧面，临界情况就是让电子轨道与半径${{R}_{1}}=(2+\sqrt{3})r$的同轴等高圆柱面相切，这样求解的是磁感应强度的最小值$B$，设此时电子运动轨道半径为$R$，画出柱面以及轨迹俯视图如图所示：

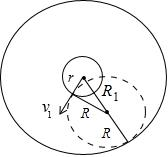
根据几何关系：$\sqrt{{{r}^{2}}+{{R}^{2}}}+R={{R}_{1}}$，将${{R}_{1}}=(2+\sqrt{3})r$代入求解出轨道半径$R=\sqrt{3}r$，

根据洛伦兹力提供向心力：${{B}_{\text{min}}}e{{v}_{1}}=m\dfrac{v_{1}^{2}}{R}$，代入${{v}_{1}}$及$R$值，求出磁感应强度的最小值${{B}_{\text{min}}}=\dfrac{1}{3r}\sqrt{\dfrac{6mU}{e}}$；

若磁感应强度的大小保持上题（$2$）得到的最小值$B$，并在金属圆柱网面与半径为${{R}_{1}}$的圆柱面之间，加竖直向下的匀强电场，电场强度为$E$（$E\geqslant \dfrac{18eH{{B}^{2}}}{25m{{\pi }^{2}}}$），同时在圆柱上端水平放置一圆形金属接收板，接收板圆心与$M$点重合，半径为${{R}_{2}}=\sqrt{7}r$，厚度忽略不计，在该金属板上接地的线路中检测到电流的电流强度为$I$，试写出电流强度$I$与电场强度$E$的关系式。

若$E\\gt \\dfrac{18eH{{B}^{2}}}{m{{\\pi }^{2}}}$，$I=Ne$；

若$\\dfrac{9eH{{B}^{2}}}{8m{{\\pi }^{2}}}\\leqslant E\\leqslant \\dfrac{18eH{{B}^{2}}}{m{{\\pi }^{2}}}$，$I=\\dfrac{mE{{\\pi }^{2}}}{18e{{B}^{2}}H}Ne$；

若$\\dfrac{18eH{{B}^{2}}}{25m{{\\pi }^{2}}}\\leqslant E\\leqslant \\dfrac{9eH{{B}^{2}}}{8m{{\\pi }^{2}}}$，$I=\\left( 1-\\dfrac{5mE{{\\pi }^{2}}}{6e{{B}^{2}}H} \\right)Ne$。

电子在圆柱的竖直方向电场中匀加速运动，加速度$a=\dfrac{eE}{m}$，在水平方向匀速圆周运动，周期$T=\dfrac{2\pi m}{eB}$。在圆柱上端水平放置一圆形金属接收板，接收板圆心与$M$点重合，半径为${{R}_{2}}=\sqrt{7}r$，

俯视图如图所示：

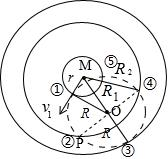
电子匀速圆周运动分别通过①②③④⑤位置，其中①⑤位置分别为刚出和回到金属圆柱网面，其中②④位置为轨迹与接收板边缘的交点，根据题意以及几何关系可以证明

$\angle MOP=\dfrac{\pi }{2}$，所以①至②过程圆弧对应圆心角、④至⑤过程圆弧对应圆心角均为$\dfrac{\pi }{3}$，由$H=\dfrac{1}{2}a{{t}^{2}}$，把$E$最小值以及$a$值代入，最下端的电子达到接收板的时间小于$\dfrac{5}{6}T$，

若最下端电子在$\dfrac{2}{3}T$时刻到达接收板，则$\dfrac{1}{2}\cdot \dfrac{eE}{m}\cdot \dfrac{16{{\pi }^{2}}{{m}^{2}}}{9{{e}^{2}}{{B}^{2}}}=H$，则$E=\dfrac{9eH{{B}^{2}}}{8m{{\pi }^{2}}}$，

若最下端电子在$\dfrac{1}{6}T$时刻到达接收板，则$\dfrac{1}{2}\cdot \dfrac{eE}{m}\cdot \dfrac{{{\pi }^{2}}{{m}^{2}}}{9{{e}^{2}}{{B}^{2}}}=H$，则$E=\dfrac{18eH{{B}^{2}}}{m{{\pi }^{2}}}$，

第一种情况，若最下端电子在$t\lt \dfrac{1}{6}T$内到达接收板，即$E\gt \dfrac{18eH{{B}^{2}}}{m{{\pi }^{2}}}$，则所有电子均能在轨迹①至②过程达到接收板，$I=Ne$；

第二种情况，若最下端电子在$\dfrac{1}{6}T\lt t\lt \dfrac{2}{3}T$内到达接收板，即$\dfrac{9eH{{B}^{2}}}{8m{{\pi }^{2}}}\leqslant E\leqslant \dfrac{18eH{{B}^{2}}}{m{{\pi }^{2}}}$，那么能在$\dfrac{1}{6}T$时刻到达接收板的电子离开接收板的距离${{h}_{1}}=\dfrac{1}{2}\cdot \dfrac{eE}{m}\cdot \dfrac{{{T}^{2}}}{36}=\dfrac{mE{{\pi }^{2}}}{18e{{B}^{2}}}$，

离开接收板的距离小于${{h}_{1}}$的电子能在轨迹①至②过程达到接收板，所以$I=\dfrac{{{h}_{1}}}{H}Ne=\dfrac{mE{{\pi }^{2}}}{18e{{B}^{2}}H}Ne$；

第三种情况，若最下端电子在$\dfrac{2}{3}T\lt t\lt \dfrac{5}{6}T$内到达接收板，即$\dfrac{18eH{{B}^{2}}}{25m{{\pi }^{2}}}\leqslant E\leqslant \dfrac{9eH{{B}^{2}}}{8m{{\pi }^{2}}}$，那么能在$\dfrac{2}{3}T$时刻到达接收板的电子离开接收板的距离${{h}_{2}}=\dfrac{1}{2}\cdot \dfrac{eE}{m}\cdot \dfrac{4{{T}^{2}}}{9}=\dfrac{8mE{{\pi }^{2}}}{9e{{B}^{2}}}$，

离开接收板的距离大于${{h}_{2}}$的电子能在轨迹④至⑤过程达到接收板，

离开接收板的距离小于${{h}_{1}}$的电子能在轨迹①至②过程达到接收板，

所以$I=\dfrac{(H-{{h}_{2}})+{{h}_{1}}}{H}\cdot Ne=\left( 1-\dfrac{5mE{{\pi }^{2}}}{6e{{B}^{2}}H} \right)Ne$。

综上所述，电流强度$I$与电场强度$E$的关系式为：

若$E\gt \dfrac{18eH{{B}^{2}}}{m{{\pi }^{2}}}$，$I=Ne$；

若$\dfrac{9eH{{B}^{2}}}{8m{{\pi }^{2}}}\leqslant E\leqslant \dfrac{18eH{{B}^{2}}}{m{{\pi }^{2}}}$，$I=\dfrac{mE{{\pi }^{2}}}{18e{{B}^{2}}H}Ne$；

若$\dfrac{18eH{{B}^{2}}}{25m{{\pi }^{2}}}\leqslant E\leqslant \dfrac{9eH{{B}^{2}}}{8m{{\pi }^{2}}}$，$I=\left( 1-\dfrac{5mE{{\pi }^{2}}}{6e{{B}^{2}}H} \right)Ne$。