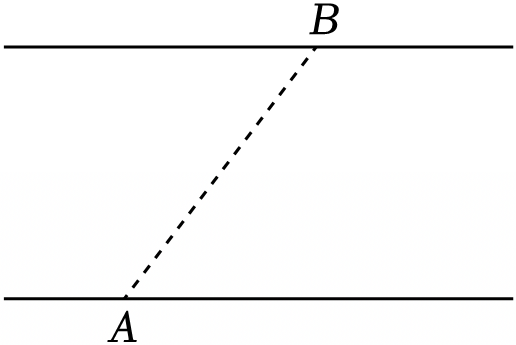
如图所示，某条河流两岸笔直，河水流速不变，甲、乙两艘船在静水中航行的速度分别为$4\;\rm m/s$和$2.4\;\rm m/s$，两船从同一渡口$A$同时向河对岸开去，甲船用最短时间渡河，乙船以最短航程渡河，结果两船均沿直线先、后抵达对岸的同一渡口$B$，乙船比甲船晚到$64\;\rm s$，下列说法正确的是$(\qquad)$

水流的速度大小为$2.5\\;\\rm m/s$

乙船渡河的时间为$120\\;\\rm s$

两渡口的距离为$180\\;\\rm m$

两岸的距离为$121\\;\\rm m$

$\rm A$．由题意可知，甲、乙两船的实际速度方向相同，根据如图所示

由几何关系有$\tan\theta=\dfrac{v_{水}}{v_{甲}}$，$\cos\theta= \dfrac{v_{乙}}{v_{水}}$，解得$\sin\theta= \dfrac{v_{乙}}{v_{甲}}=\dfrac{3}{5}$，所以$\dfrac{v_{水}}{v_{甲}}=\dfrac{3}{4}$，解得$v_{水}=3\;\rm m/s$，故$\rm A$错误；

$\rm B$．设乙船渡河的时间为$t_{乙}$，则有$\dfrac{v_{甲}(t_{乙}-64\;\rm s)}{\cos\theta} =v_{乙}t_{乙}\tan\theta$，解得$t_{乙}=100\;\rm s$，故$\rm B$错误；

$\rm C$．两渡口的距离$s=v_{乙}t_{乙}\tan\theta$，解得$s=180\;\rm m$，故$\rm C$正确；

$\rm D$．两岸的距离$d=s\cos\theta$，解得$d=144\;\rm m$，故$\rm D$错误。

故选：$\rm C$。