如图所示，一艘炮艇沿长江由西向东快速行驶，在炮艇上发射炮弹射击北岸的目标。已知炮艇向正东行驶的速度大小为$v_{1}$，炮艇静止时炮弹的发射速度大小为$v_{2}$，炮艇所行进的路线离射击目标的最近距离为$d$，不计空气阻力的影响，要想命中目标且炮弹在空中飞行时间最短，则$(\qquad)$

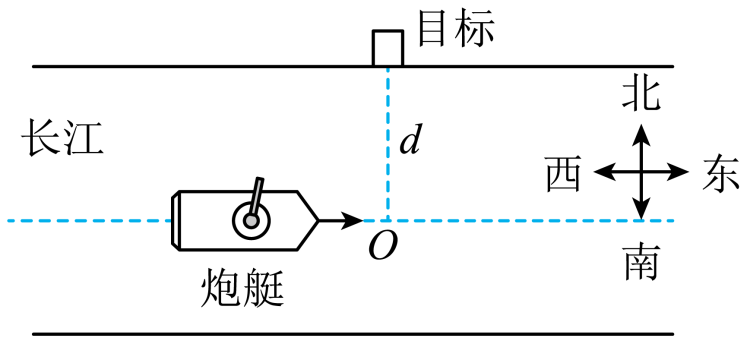
当炮艇前进至$O$点时垂直于运动方向向北发射炮弹刚好能击中目标

炮艇距离目标为$\\dfrac{v_{1}}{v_{2}}d$时发射炮弹

炮艇距离目标为$\\sqrt{v_{1}^{2}+v_{2}^{2}}\\dfrac{d}{v_{2}}$时发射炮弹

炮弹在空中飞行的最短时间是$\\dfrac{d}{v_{1}}$

$\rm A$．当炮艇前进至$O$点时垂直于运动方向向北发射炮弹，炮弹参与沿着河岸的运动和垂直于河岸的两个运动，最后炮弹将落在目标的东方，$\rm A$错误；

$\rm D$．在垂直河岸速度最大时，飞行时间最短，且最短时间为$t=\dfrac{d}{v_{2}}$，$\rm D$错误；

$\rm BC$．在空中飞行时间最短时，发射点位置到$O$点的距离$x=v_{1}t=v_{1}\dfrac{d}{v_{2}}$

因此发射点位置到目标的距离$s=\sqrt{x^{2}+d^{2}}=\sqrt{v_{1}^{2}+v_{2}^{2}}\dfrac{d}{v_{2}}$

$\rm B$错误，$\rm C$正确。

故选：$\rm C$。