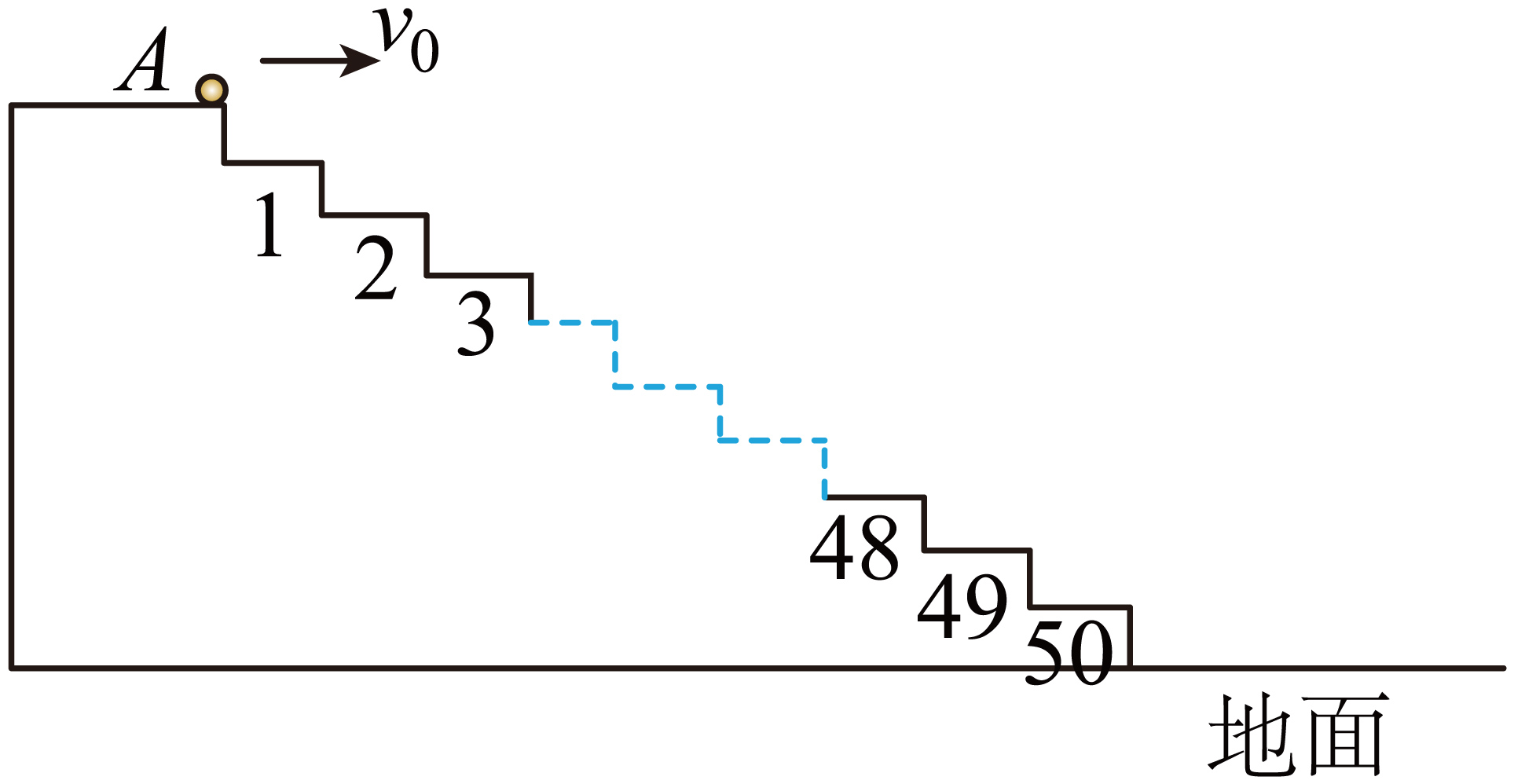
要使小球直接落到地面，求初速度$v_{0}$的范围；

$v_{0} \\geqslant 5\\sqrt{6}\\;\\rm \\text{m/s}$

小球做平抛运动，轨迹如图

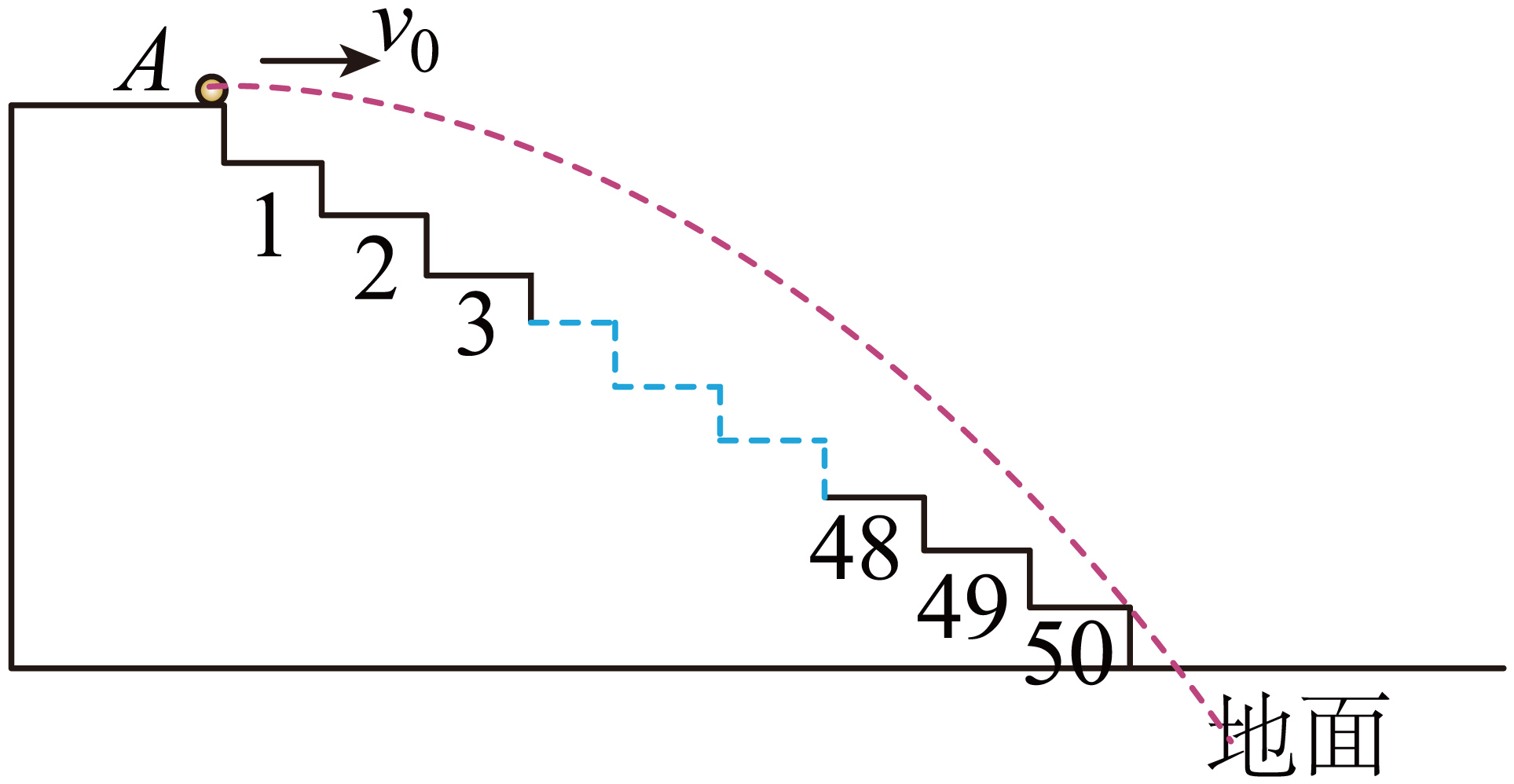
可知小球刚好直接落到地面时需擦过第$50$级台阶最右端，由平抛运动规律$50h=\dfrac{1}{2}gt_{1}^{2}$，$50\;{\rm s}=v_{0\min }t_{1}$

解得$v_{0\min}=5\sqrt{6}\;\rm \text{m/s}$

故要使小球直接落到地面，求初速度$v_{0}$的范围为$v_{0} \geqslant 5\sqrt{6}\;\rm \text{m/s}$。

若$v_{0}=8\;\rm m/s$，求小球首先落到哪一级台阶上；

第$22$级

若$v_{0}=8\;\rm m/s$，设小球会落到第$n$级台阶上，由平抛运动规律$nh=\dfrac{1}{2}gt_{2}^{2}$，$ns=v_{0}t_{2}$

解得$n=\dfrac{64}{3}$，$n$取整数后得，$n=22$，故小球会落在第$22$级台阶上。

若将小球斜向上抛出，恰好能够直接打到第$50$级台阶最右端，求最小初速度的大小。

$v_{0\\min }'=10\\;\\rm m/s$

设小球的初速度方向与水平方向夹角为$\theta$，如图

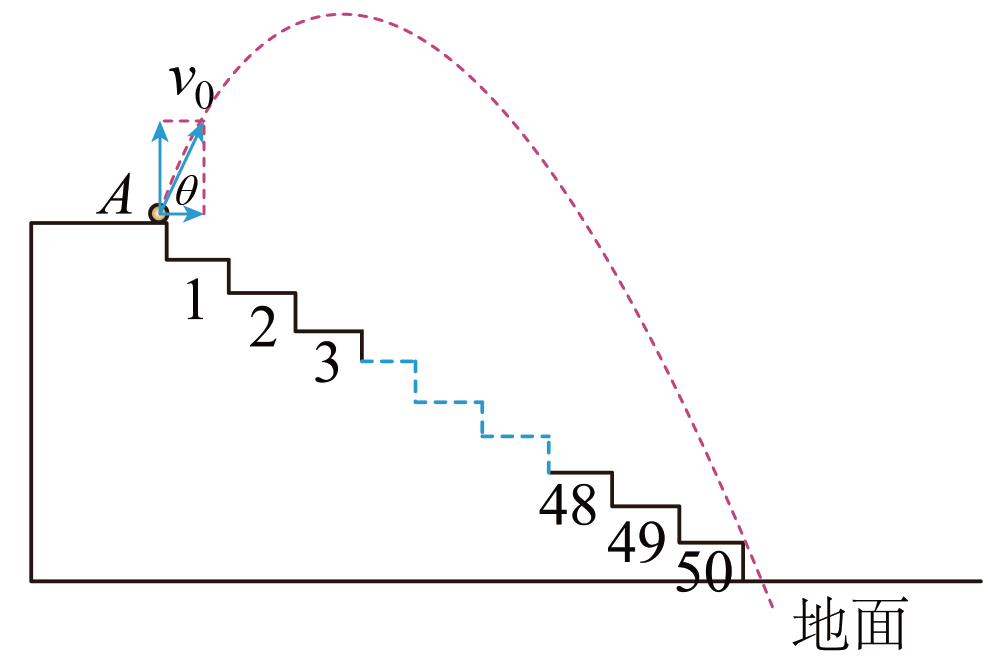
则在竖直方向上$50h=-v_{0}'t\sin\theta+\dfrac{1}{2}gt^{2}$

水平方向上有$50\;{\rm s}=v_{0}'t\cos \theta$

联立得$v_{0}'^{2}=\dfrac{1500}{5\cos 2\theta+5\sqrt{3}\sin 2\theta+5}=\dfrac{1500}{10\sin(2\theta+30{^\circ})+5}$

所以当$\theta=30^\circ$时，抛出时的初速度最小，$v_{0\min }'=10\;\rm m/s$。