如图所示，间距为$L$的光滑平行金属导轨水平固定，导轨左端连接有阻值为$R$的定值电阻。一在导轨上垂直于导轨放置一金属棒$MN$，金属棒及导轨电阻不计。现在金属棒与定值电阻之间加一边界为矩形的匀强磁场，且知矩形长为$a$、宽为$b(b \gt L)$，磁场磁感应强度大小为$B$，方向垂直导轨平面向下。若使磁场以速度$v_{0}$平行导轨向右匀速运动，直至金属棒穿越磁场，则下列说法中正确的是$(\qquad)$

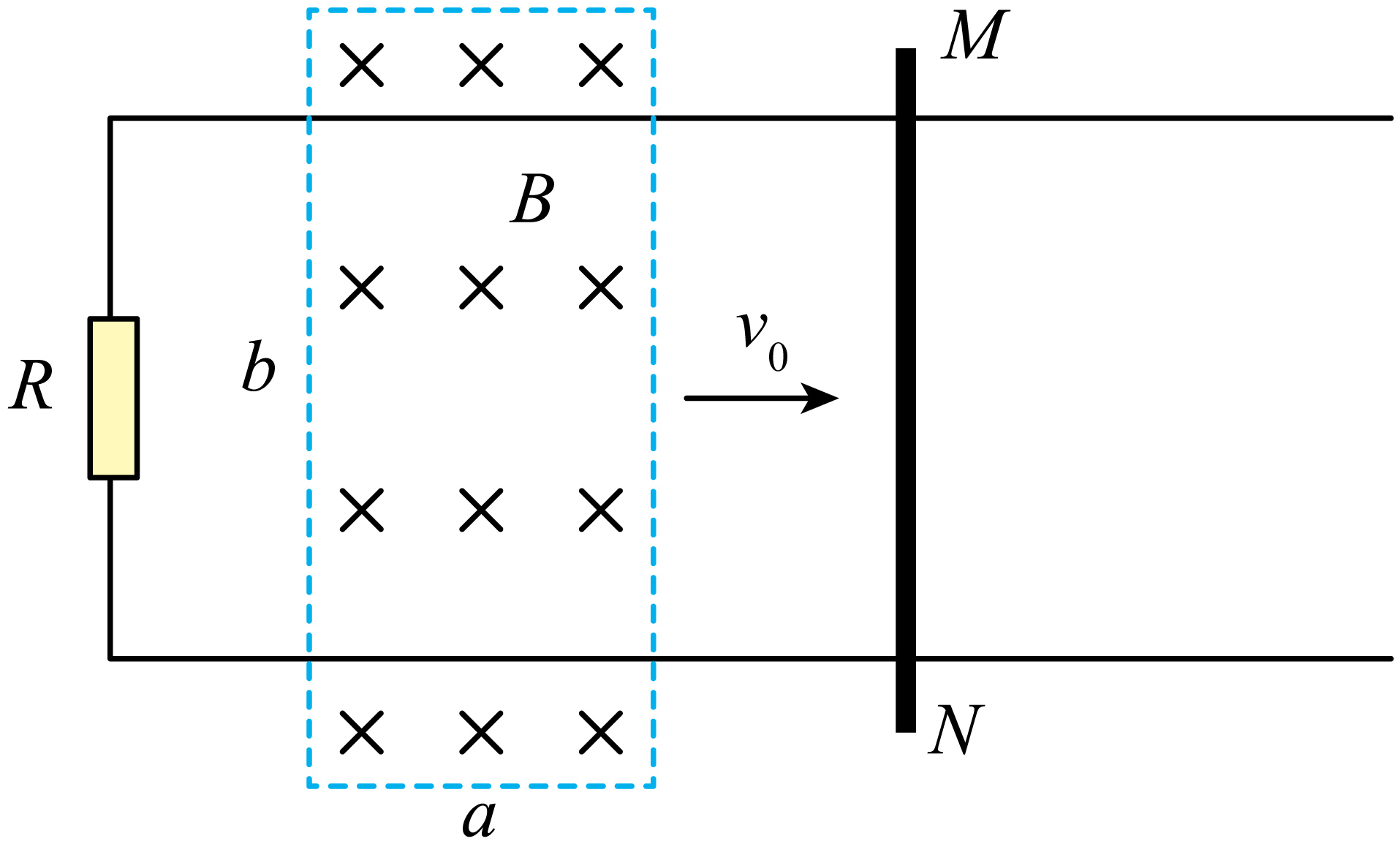
金属棒穿越磁场的过程中，有自$M$向$N$的感应电流

金属棒穿越磁场的过程中，金属棒中的感应电流在不断增大

若增大磁场运动速度$v_{0}$，则金属棒脱离磁场时的速度也增大

金属棒穿越磁场的整个过程，流过电阻的电荷量为$\\dfrac{BLa}{R}$

$\rm A$．导体棒进入磁场时相对磁场向左运动，由右手定则可知此时导体棒中的感应电流由$M$向$N$，故$\rm A$正确；

$\rm B$．金属棒在安培力作用下向右加速运动，但相对磁场的速度由$v_{0}$逐渐减小，动生电动势亦逐渐减小，所以金属棒中的感应电流逐渐减小，故$\rm B$错误；

$\rm CD$．设金属棒的质量为$m$，由动量定理可得$B\overline{I}L\Delta t=mv$

其中金属棒穿越磁场的整个过程，流过电阻的电荷量为$q=\overline{I}\Delta t=\dfrac{\overline{E}}{R}\Delta t=\dfrac{\Delta\Phi}{R}=\dfrac{BLa}{R}$

故$\dfrac{B^{2}L^{2}a}{R}=mv$

解得金属棒离开磁场时的速度为$v=\dfrac{B^{2}L^{2}a}{mR}$，可见其与$v_{0}$无关，故$\rm C$错误，$\rm D$正确。

故选：$\rm AD$。