如图甲所示，两条相距为$d$的足够长光滑平行金属导轨固定在水平面内，导轨左端与一阻值为$R$的电阻相连，整个装置处于磁感应强度大小为$B$、方向垂直于导轨所在平面的匀强磁场中。质量为$m$、长度为$d$的导体棒$ab$静置在导轨上，以此位置为坐标原点，沿导轨向右为正方向建立$x$轴。某时刻给导体棒$ab$瞬时冲量使其获得向右的初速度$v_{0}$，同时对导体棒$ab$施加与导轨平行的水平方向的力，使导体棒$ab$向右做减速运动直至停止，导体棒$ab$速度随位移变化的图像如图乙所示。不计导体棒$ab$及金属导轨的电阻，下列说法正确的是$(\qquad)$

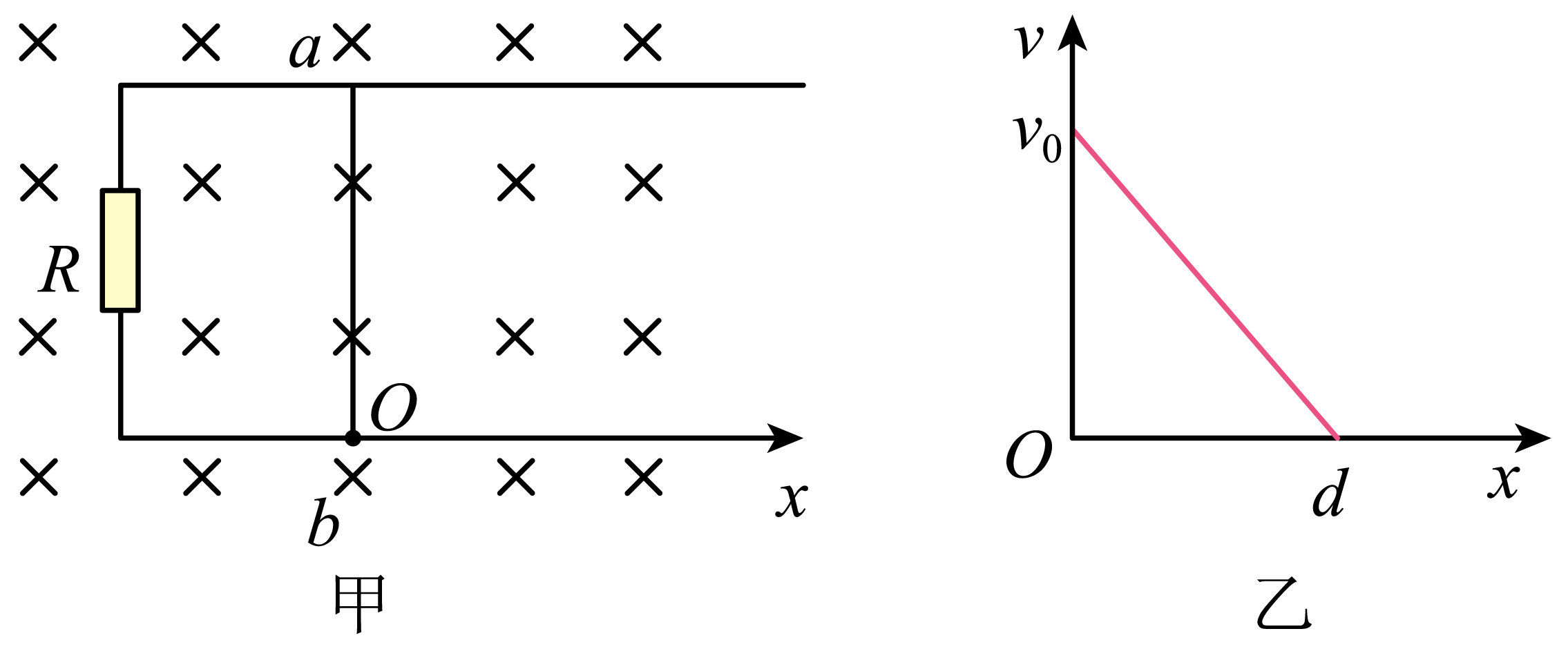
导体棒$ab$做匀减速直线运动

在$x=0$位置导体棒所受的安培力大小为$\\dfrac{B^{2}d^{2}v_{0}}{R}$，方向水平向右

这一过程中电阻$R$放出的热量为$\\dfrac{B^{2}d^{3}v_{0}}{2R}$

水平力对导体棒$ab$做功为$\\dfrac{B^{2}d^{3}v_{0}}{R}-\\dfrac{1}{2}mv_{0}^{2}$

$\rm A$．由速度$—$位移图像可知，导体棒运动过程中加速度是变化的，故$\rm A$错误；

$\rm B$．$x=0$时，导体棒$ab$产生的电动势为$E=Bdv_{0}$

电流为$I=\dfrac{E}{R}$

安培力为$F=BId$

联立解得$F=\dfrac{B^{2}d^{2}v_{0}}{R}$

方向水平向左，故$\rm B$错误；

$\rm C$．安培力做负功把其他形式的能转化为电能，被电阻$R$消耗放热，由$F=$ $\dfrac{B^{2}d^{2}v}{R}$可知，$F ∝ v$，可作出$F$和位移$x$的关系图像，如图所示

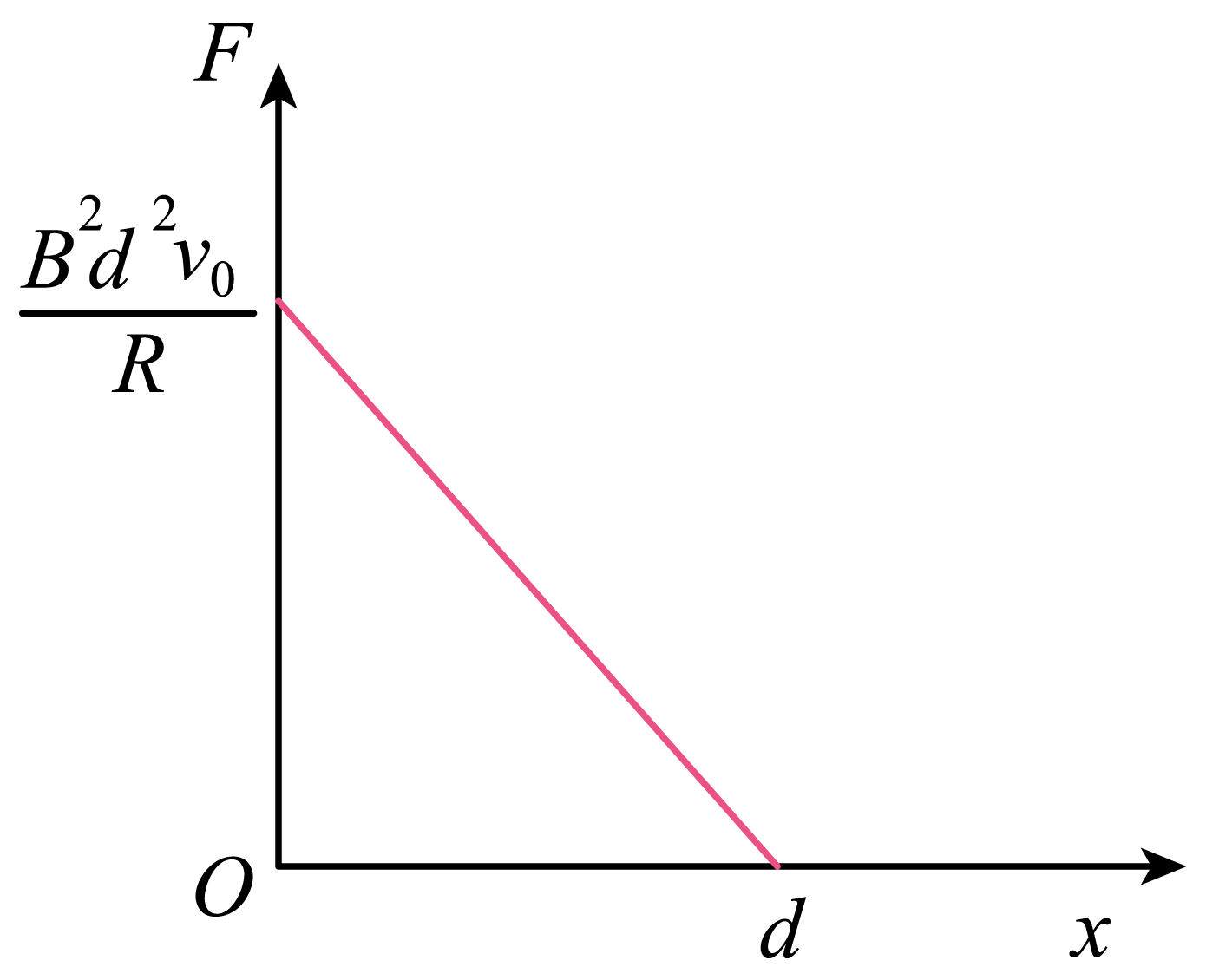
图像围成的面积等于克服安培力做功，所以$Q=\left| W_{安} \right|=\dfrac{B^{2}d^{3}v_{0}}{2R}$，故$\rm C$正确；

$\rm D$．根据动能定理得$W-\dfrac{B^{2}d^{3}v_{0}}{2R}=0 -$ $\dfrac{1}{2}mv_{0}^{2}$

解得$W=\dfrac{B^{2}d^{3}v_{0}}{2R}-\dfrac{1}{2}mv_{0}^{2}$，故$\rm D$错误。

故选：$\rm C$。