如图所示，两根平行光滑金属导轨固定在同一水平面内，其左端接有定值电阻$R$，建立$Ox$轴平行于金属导轨，在$x\gt 0$的区域内存在着垂直导轨平面向下的磁场，磁感应强度$B$随坐标$x$分布规律为$B=5x(\rm T)$，金属棒$ab$在外力作用下从$x=0$处沿导轨向右运动，经过$x_{1}$、$x_{2}$、$x_{3}$，$Ox_{1}=x_{1}x_{2}=x_{2}x_{3}$，电阻$R$的功率始终保持不变，不计导轨和金属棒的电阻，则在$x_{1}x_{2}$和$x_{2}x_{3}$过程中$(\qquad)$

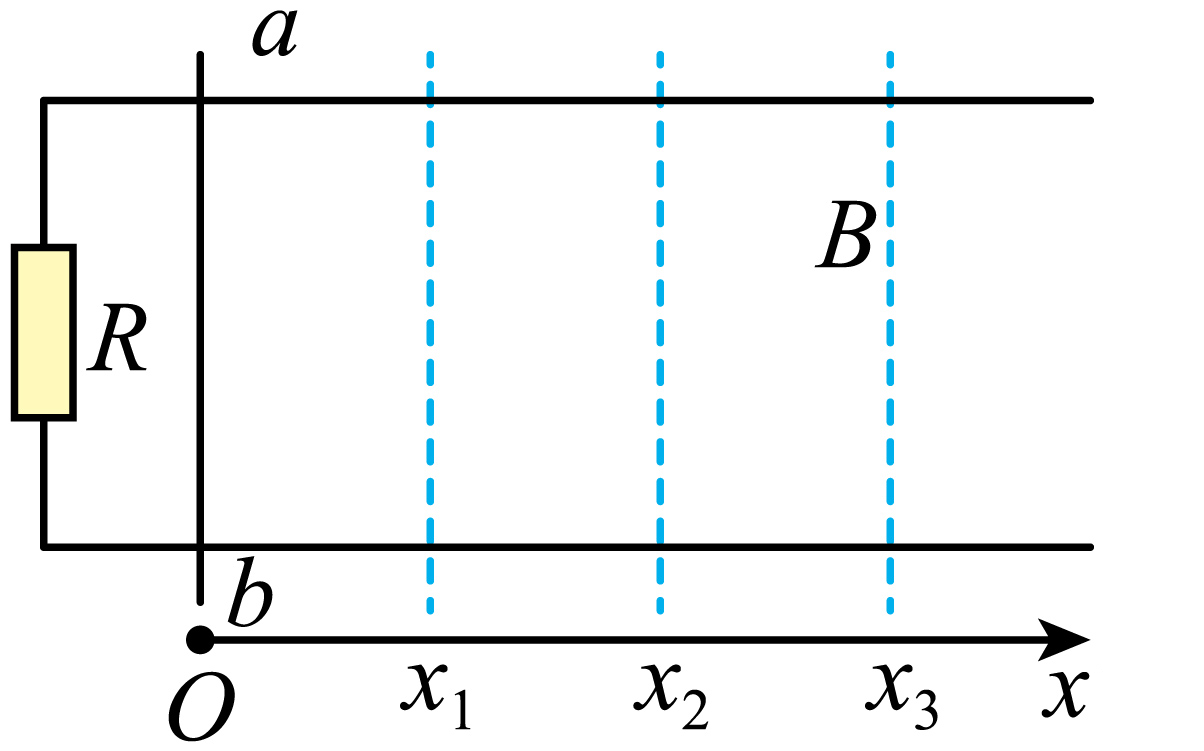
金属棒$a$端电势低于$b$端

金属棒产生的电动势逐渐增大

通过电阻$R$的电量之比为$3:5$

金属棒运动时间之比为$1:2$

$\rm A$．导体棒相当于电源，电源的电流由负极流向正极，根据右手定则，可知导体棒中的电流从$b$流过$a$，故$a$端相当于电源的正极，$b$端相当于电源的负极，则$a$端电势高于$b$端电势，故$\rm A$错误；

$\rm B$．由题知，电阻$R$的功率始终保持不变，根据$P=\dfrac{E^{2}}{R}$

解得$E=\sqrt{PR}$

金属棒产生的电动势$E$保持不变，故$\rm B$错误；

$\rm C$．根据$\overline{E}=\dfrac{\Delta\Phi}{\Delta t}$，$\overline{I}=\dfrac{\overline{E}}{R}$，$q=\overline{I}\Delta t$

联立解得$q=\dfrac{\Delta\Phi}{R}$

故$q_{1}:q_{2}=\Delta\Phi_{1}:\Delta\Phi_{2}$

根据磁感应强度$B$随坐标$x$分布规律为$B=5x(\rm T)$，作出$B − x$图像，如图所示

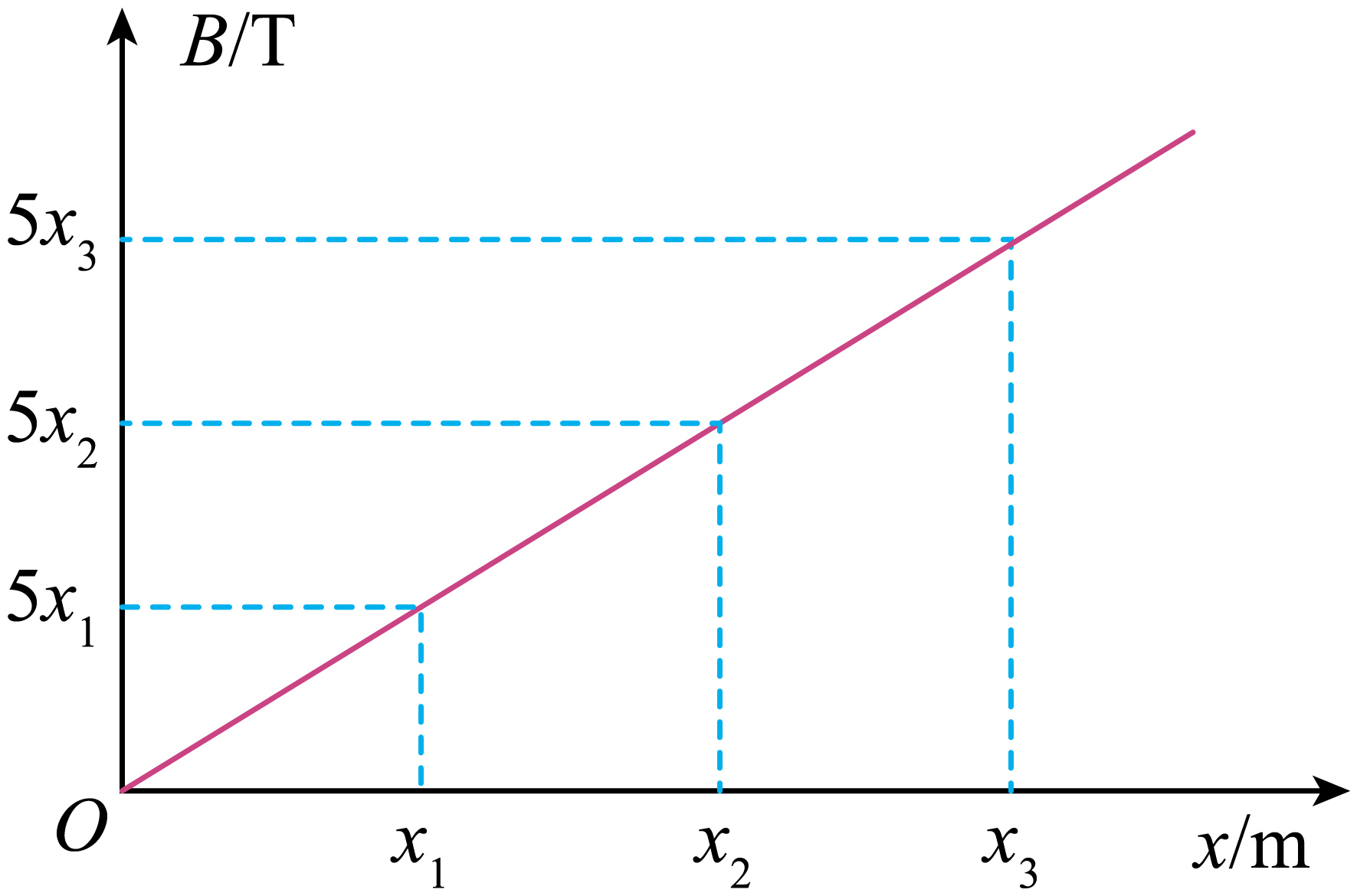
设两根平行光滑金属导轨间距为$L$，则从$x_{1}$到$x_{2}$，磁通量为$\Delta\Phi_{1}=\dfrac{5x_{1}+5x_{2}}{2}\left( x_{2}-x_{1} \right)L$

从$x_{2}$到$x_{3}$磁通量为$\Delta\Phi_{2}=\dfrac{5x_{2}+5x_{3}}{2}\left( x_{3}-x_{2} \right)L$

设$Ox_{1}=x_{1}x_{2}=x_{2}x_{3}=x_{0}$，可得$x_{1}=x_{0}$，$x_{2}=2x_{0}$，$x_{3}=3x_{0}$，则磁通量化简为$\Delta\Phi_{1}=\dfrac{15x_{0}^{2}}{2}L$，$\Delta\Phi_{2}=\dfrac{25}{2}x_{0}^{2}L$

故$q_{1}:q_{2}=\Delta\Phi_{1}:\Delta\Phi_{2}=\dfrac{15x_{0}^{2}L}{2}:\dfrac{25x_{0}^{2}L}{2}=3:5$，故$\rm C$正确；

$\rm D$．由$\rm B$项，可知金属棒产生的电动势$E$保持不变，则电流$I=\dfrac{E}{R}$

可知电流$I$保持不变；

根据$q=I\Delta t$

可得$\Delta t=\dfrac{q}{I}$

故$\Delta t_{1}:\Delta t_{2}=q_{1}:q_{2}=3:5$，故$\rm D$错误。

故选：$\rm C$。