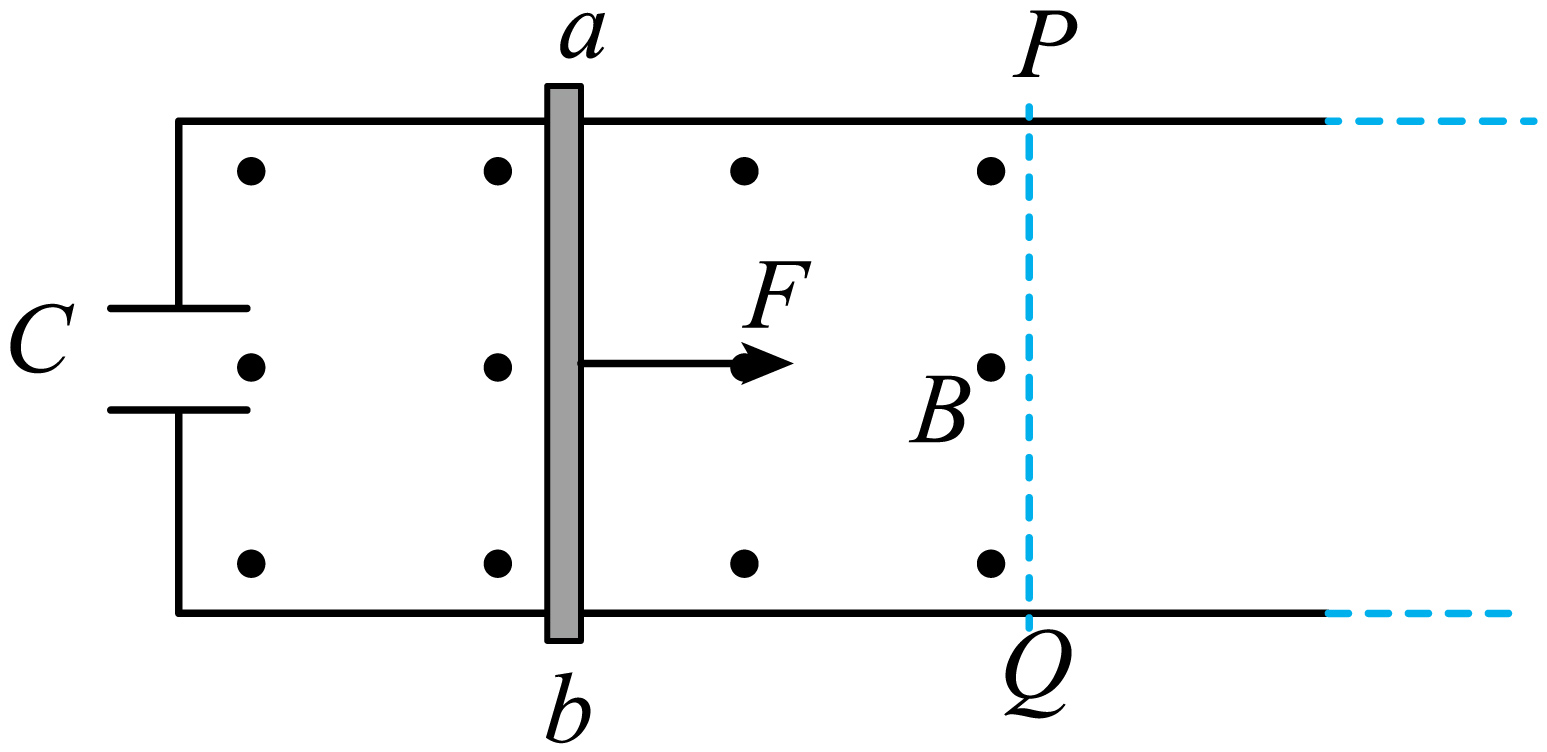
如图所示，间距为$L$的水平光滑长导轨，左端接有一个电容器，电容为$C$（不会被击穿），在$PQ$虚线的左侧有竖直向上的匀强磁场，磁感应强度大小为$B$。质量为$m$的金属杆$ab$静置在导轨上，距离虚线$PQ$的距离是$d$，金属杆在水平向右恒力$F$的作用下，开始向右运动，不计导轨与金属杆的电阻，下列说法正确的是 $(\qquad)$

金属杆$ab$先做加速度不断减小的加速运动，最终匀速运动

金属杆$ab$的运动可能是先从加速到匀速再到加速

金属杆$ab$运动到达虚线$PQ$的时间$t=2d\\sqrt{\\dfrac{m+C{{B}^{2}}{{L}^{2}}}{F}}$

电容器能带的最多电量是$CBL\\sqrt{\\dfrac{2dF}{m+C{{B}^{2}}{{L}^{2}}}}$

金属棒向右运动，切割磁感应线产生电动势$E$，给电容器充电，设在$t\sim t+\Delta t$的时间里，电容器充电量为$\Delta q$，则$\Delta q=CE=CBL\Delta v$，则充电电流为$i=\dfrac{\Delta q}{\Delta t}=CBL\dfrac{\Delta v}{\Delta t}=CBLa$，对金属棒列牛顿第二定律方程$F-BLi=ma$

得$a=\dfrac{F}{m+C{{B}^{2}}{{L}^{2}}}$，上式说明金属棒做初速度为零的匀加速直线运动，由$x=\dfrac{1}{2}a{{t}^{2}}$，可得$t=\sqrt{\dfrac{2d}{a}}$，得$t=\sqrt{\dfrac{2d}{a}}=\sqrt{\dfrac{2d(m+C{{B}^{2}}{{L}^{2}})}{F}}$，再由$q=CE=CBLv=CBLat$，得金属杆最终出磁场时，电容器带电量最大，带电量为${{q}_{\max }}=CBL\sqrt{\dfrac{2dF}{m+C{{B}^{2}}{{L}^{2}}}}$。

故选：$\rm D$。