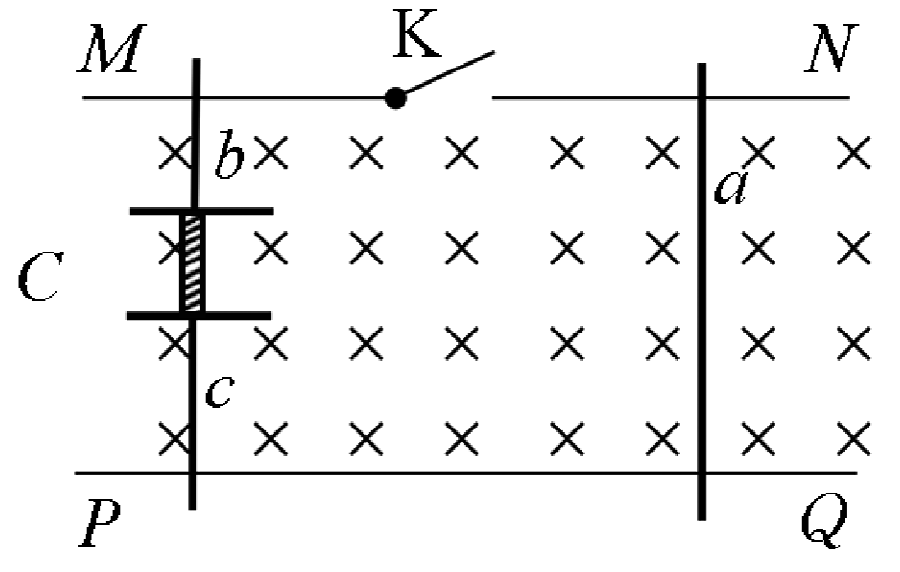
如图所示，足够长的光滑平行金属导轨$MN$、$PQ$固定在水平地面上，导轨$MN$上有一电键$K$，导轨$MN$、$PQ$间有磁感应强度为$B$的竖直向下的匀强磁场，导轨间距为$3d$。现有一间距为$d$、电容为$C$的平行金属板（厚度不计）电容器，两金属板间用一绝缘细杆连接并固定，金属板两侧用金属杆$b$、$c$垂直相连，它们总质量为$m$，并垂直于导轨静置于电键$K$左端的导轨上；电键$K$右端的导轨上垂直放置另一质量为$m$的金属杆$a$。若电容器的带电量为${{q}_{0}}$，闭合电键$K$，当整个系统达到稳定后（杆均未经过电键$K$）$(\qquad)$

电容器最终带电量为$\\dfrac{m{{q}_{0}}}{m+13{{B}^{2}}{{d}^{2}}}$

电容器最终带电量为$\\dfrac{13C{{B}^{2}}{{d}^{2}}{{q}_{0}}}{m+13{{B}^{2}}{{d}^{2}}}$

金属杆$a$的最终速度为$\\dfrac{2Bd{{q}_{0}}}{m+13{{B}^{2}}{{d}^{2}}}$

金属杆$a$的最终速度为$\\dfrac{3Bd{{q}_{0}}}{m+13{{B}^{2}}{{d}^{2}}}$

由动量定理，对$a$有$B\left( 3d \right)\left( {{q}_{0}}-q \right)=m{{v}_{a}}-0$

对$b$、$c$及电容器系统有$B\left( 2d \right)\left( {{q}_{0}}-q \right)=m{{v}_{b}}-0$

又因$q=C\left[ B\left( 3d \right){{v}_{a}}+B\left( 2d \right){{v}_{b}} \right]$

联立解之得$q=\dfrac{13C{{B}^{2}}{{d}^{2}}{{q}_{0}}}{m+13C{{B}^{2}}{{d}^{2}}}$，${{v}_{a}}=\dfrac{3Bd{{q}_{0}}}{m+13C{{B}^{2}}{{d}^{2}}}$。

故选：$\rm BD$。